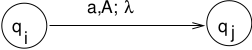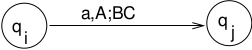1. PDAs and Context Free Languages¶

Now we want to show that NPDA's and CFG both represent CFL's. Show that we can take any CFG and construct a NPDA and vice versa.

Theorem: For any CFL $L$ not containing $\lambda$, $\exists$ a NPDA $M$ such that $L = L(M)$.

Proof (sketch)

Given ($\lambda$ -free) CFL $L$.

$\Rightarrow \exists$ CFG $G$ such that $L = L(G)$.

$\Rightarrow \exists G'$ in GNF, such that $L(G) = L(G')$.

$G' = (V,T,S,P)$. All productions in $P$ are of the form:

$A \rightarrow ax$

$A \in V, a \in T, x \in V^*$

Construct NPDA $M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)$

$Q = \{q_0, q_1, q_f\}, \Sigma = T, \Gamma = V \cup \{z\}, F = \{q_f\}$

1. $M$ starts by putting $S$ on the stack

2. For each production

$A \rightarrow a X_1 X_2 \ldots X_n$

put $(q_1, X_1 X_2 \ldots X_n)$ in $\delta(q_1, a, A)$

(Pop $A$ from the stack, read "a" from tape, and push $X_1 X_2 \ldots X_n$ onto the stack)

3. Accept if $S \stackrel{*}{\Rightarrow} w \in \Sigma^*$ (all variables on the stack are replaced by terminals or $\lambda$)

Show $w \in L(G')$ iff $w \in L(M)$. QED.

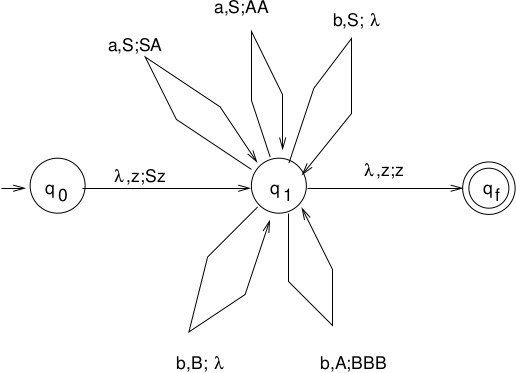
Example 1

Let $G' = (V,T,S,P), P =$ | $S \rightarrow aSA\ |\ aAA\ |\ b$ | $A \rightarrow bBBB$ | $B \rightarrow b$

QUESTION: Is this grammar in GNF? Yes.

Trace abbbbb in grammar and pda.

Note

Argue why $w \in L(G')$ iff $w \in L(M)$. QED.

Now we want to show that given an NPDA, we can construct a CFG. But first, we will show a result to make the next proof easier.

Theorem: Given a NPDA $M$, $\exists$ a NPDA $M'$ such that all transitions have the form $\delta(q_i, a, A) = \{c_1, c_2, \ldots c_n\}$ where

Each move either increases or decreases stack contents by a single symbol.

Proof: (sketch)

Theorem: If $L = L(M)$ for some NPDA $M$, then $L$ is a CFL.

Proof:

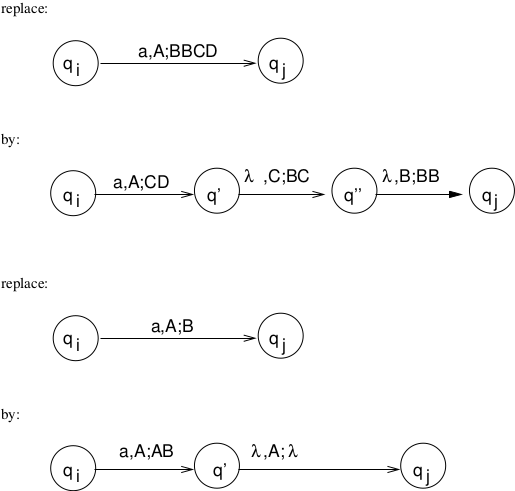
Given NPDA $M$, first, construct an equivalent NPDA $M'$ that will be easier to work with. Construct $M'$ such that

1. $M'$ accepts if stack is empty

2. Each move increases or decreases stack content by a single symbol. (Can only push 2 variables or no variables with each transition.)

$M' = (Q, \Sigma, \Gamma, \delta, q_0, z, F)$

Construct $G = (V,\Sigma, S, P)$ where

$V = \{(q_icq_j)\ |\ q_i, q_j \in Q, c \in \Gamma \}$

(Some of these variables will be useless.)

$(q_icq_j)$ represents "starting at state $q_i$ the stack contents are $cw, w \in \Gamma^*$, some path is followed to state $q_j$ and the contents of the stack are now $w$".

Goal: $(q_0zq_f)$ which will be the start symbol in the grammar.

Meaning: We start in state $q_0$ with $z$ on the stack and process the input tape. Eventually we will reach the final state $q_f$ and the stack will be empty. (Along the way we may push symbols on the stack, but these symbols will be popped from the stack).

(NOTE: Machine accepts by empty stack, but it is such that there is only 1 final state in which the machine accepts by final state.)

To construct the productions in P:

1) Replace

by

$$(q_iAq_j) \rightarrow a$$

where the stack changes are:

$$\begin{split}\begin{array}{lcclc} & q_i & \ \ (\mbox{some path}\ \rightarrow) \ \ & &q_j \\ \\ \mbox{stack:} & A && \mbox{stack:} & \\ & X_1 & && X_1 \\ & X_2 &&& X_2 \\ & \underline{X_n} &&& \underline{X_n} \\ \end{array}\end{split}$$

2) Replace

by

$$(q_iAq_k) \rightarrow a(q_jBq_l)(q_lCq_k)\ \mbox{for all}\ q_l, q_k \in Q$$

$$\begin{split}\begin{array}{ccccccc} q_i & \ \ (\mbox{path}\ \rightarrow) \ \ & q_j &\ \ (\mbox{path}\ \rightarrow) \ \ & q_l &\ \ (\mbox{path}\ \rightarrow) \ \ & q_k \\ \\ &&B&& \\ A && C &&C \\ X_1 & & X_1 & & X_1 & & X_1 \\ X_2 && X_2 && X_2 && X_2 \\ \underline{X_n} &&\underline{X_n} &&\underline{X_n} &&\underline{X_n}\\ \end{array}\end{split}$$

This will create some useless variables, but that's ok.

Must show that the constructed grammar $G$ is such that $L(G) = L(M')$. That is, $w \in L(G) \mbox{iff}\ w \in L(M)$. (see book) QED.

Example 2

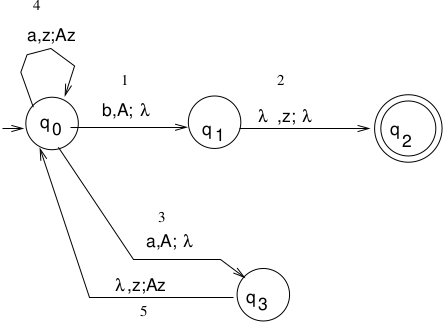
$L(M) = \{aa^*b\}$, $M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)$, $Q = \{q_0, q_1, q_2, q_3\}$, $\Sigma = \{a, b\}, \Gamma = \{A, z\}$, $F = \{\}$. $M$ accepts by empty stack.

Construct the grammar $G = (V,T,S,P)$,

$V = \{(q_0Aq_0), (q_0zq_0), (q_0Aq_1), (q_0zq_1), \ldots \}$

NOTE: some variables may be useless.

$T = \Sigma$

$S = (q_0zq_2)$

$P =$

$$\begin{split}\begin{array}{crl} \mbox{From transition 1} & (q_0Aq_1) \rightarrow & b \\ \\ \mbox{From transition 2} & (q_1zq_2) \rightarrow & \lambda \\ \\ \mbox{From transition 3} & (q_0Aq_3) \rightarrow & a \\ \\ \mbox{From transition 4} & (q_0zq_0) \rightarrow & a(q_0Aq_0)(q_0zq_0)| \\ & & a(q_0Aq_1)(q_1zq_0)| \\ & & a(q_0Aq_2)(q_2zq_0)| \\ & & a(q_0Aq_3)(q_3zq_0) \\ & (q_0zq_1) \rightarrow & a(q_0Aq_0)(q_0zq_1)| \\ & & a(q_0Aq_1)(q_1zq_1)| \\ & & a(q_0Aq_2)(q_2zq_1)| \\ & & a(q_0Aq_3)(q_3zq_1) \\ & (q_0zq_2) \rightarrow & a(q_0Aq_0)(q_0zq_2)| \\ & & a(q_0Aq_1)(q_1zq_2)| \\ & & a(q_0Aq_2)(q_2zq_2)| \\ & & a(q_0Aq_3)(q_3zq_2) \\ & (q_0zq_3) \rightarrow & a(q_0Aq_0)(q_0zq_3)| \\ & & a(q_0Aq_1)(q_1zq_3)| \\ & & a(q_0Aq_2)(q_2zq_3)| \\ & & a(q_0Aq_3)(q_3zq_3) \\ \mbox{From transition 5} & (q_3zq_0) \rightarrow & (q_0Aq_0)(q_0zq_0)| \\ & & (q_0Aq_1)(q_1zq_0)| \\ & & (q_0Aq_2)(q_2zq_0)| \\ & & (q_0Aq_3)(q_3zq_0) \\ & (q_3zq_1) \rightarrow & (q_0Aq_0)(q_0zq_1)| \\ & & (q_0Aq_1)(q_1zq_1)| \\ & & (q_0Aq_2)(q_2zq_1)| \\ & & (q_0Aq_3)(q_3zq_1) \\ & (q_3zq_2) \rightarrow & (q_0Aq_0)(q_0zq_2)| \\ & & (q_0Aq_1)(q_1zq_2)| \\ & & (q_0Aq_2)(q_2zq_2)| \\ & & (q_0Aq_3)(q_3zq_2) \\ & (q_3zq_3) \rightarrow & (q_0Aq_0)(q_0zq_3)| \\ & & (q_0Aq_1)(q_1zq_3)| \\ & & (q_0Aq_2)(q_2zq_3)| \\ & & (q_0Aq_3)(q_3zq_3) \\ \end{array}\end{split}$$

Recognizing aaab in M:

$$\begin{split}\begin{eqnarray*} (q_0,aaab,z) & \vdash & (q_0,aab,Az) \\ & \vdash & (q_3,ab,z) \\ & \vdash & (q_0,ab,Az) \\ & \vdash & (q_3,b,z) \\ & \vdash & (q_0,b,Az) \\ & \vdash & (q_1, \lambda, z) \\ & \vdash & (q_2, \lambda, \lambda) \\ \end{eqnarray*}\end{split}$$

At this point stack is empty.

Derivation of string aaab in G:

$$\begin{split}\begin{eqnarray*} (q_0zq_2) & \Rightarrow & a(q_0Aq_3)(q_3zq_2) \\ & \Rightarrow & aa(q_3zq_2) \\ & \Rightarrow & aa(q_0Aq_3)(q_3zq_2) \\ & \Rightarrow & aaa(q_3zq_2) \\ & \Rightarrow & aaa(q_0Aq_1)(q_1zq_2) \\ & \Rightarrow & aaab(q_1zq_2) \\ & \Rightarrow & aaab \\ \end{eqnarray*}\end{split}$$

Meaning of first line in derivation is: $(q_0zq_2) \stackrel{*}{\Rightarrow} axy$ where $(q_0Aq_3)\stackrel{*} {\Rightarrow} x$ (which in the example above will eventually derive $a$) and $(q_3zq_2)\stackrel{*}{\Rightarrow} y$ (which in the example above will eventually derive $ab$).

Must show that the constructed grammar $G$ is such that $L(G) = L(M')$. That is, $w \in L(G)$ iff $w \in L(M)$. (see book) QED.