Deterministic Pushdown Automata¶

1. Deterministic Pushdown Automata¶

Definition: A PDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) is deterministic if for every \(q \in Q\), \(a \in \Sigma \cup \{\lambda\}\), \(b \in \Gamma\):

1. \(\delta(q, a, b)\) contains at most one element

2. if \(\delta(q, \lambda, b)\) is not empty, then \(\delta(q, c, b)\) must be empty for every \(c \in \Sigma\).

Definition: \(L\) is a deterministic context-free language (DCFL) if and only if there exists a deterministic PDA \(M\) such that \(L = L(M)\).

Example

The language \(L = \{a^nb^n | n \ge 0\}\) is a deterministic CFL.

Proof: The PDA \(M = (\{q_0, q_1, q_2\}, \{a, b\}, \{0, 1\}, \delta, q_0, 0, \{q_0\})\) with

\(\delta(q_0, a, 0) = \{(q_1, 10)\}\),
\(\delta(q_1, a, 1) = \{(q_1, 11)\}\),
\(\delta(q_1, b, 1) = \{(q_2, \lambda)\}\),
\(\delta(q_2, b, 1) = \{(q_2, \lambda)\}\),
\(\delta(q_2, \lambda, 0) = \{(q_0, \lambda)\}\)

accepts the given language. It satisfies the conditions for being deterministic.

Note that this machine DOES have \(\lambda\) transitions. The key point is that there is still only one choice (because of what is sitting on the top of the stack). In that sense, it is not merely a "free ride" transition.

Example

Our previous PDA for \(\{ww^R | w\in{\Sigma}^{+}\}, \Sigma = \{a, b\}\) is nondeterministic.

It contains these transitions:

\(\delta(q_0, a, a) = \{(q_0, aa)\}\)

\(\delta(q_0, \lambda, a) = \{(q_1, a)\}\)

This violates our conditions for determinism. (Do you see why?)

Now, this fact that we have a PDA that is not deterministic certainly does not prove that \(\{ww^R | w\in{\Sigma}^{+}\}, \Sigma = \{a, b\}\) is not a deterministic CFL.

But, there are CFL's that are not deterministic. And we will see that this is one of them. This makes intuitive sense. How can we, deterministically, know when to switch from \(w\) to \(w^R\) when scanning from left to right through the input?

Example:

\(L = \{a^nb^n|n \ge 1\} \cup \{a^nb^{2n}| n\ge 1\}\) is a CFL and not a DCFL.

Obviously, both languages are CFL. And obviously, their union is CFL. But imagine how the "obvious" PDA works: The start state transitions to the "correct" machine to recognize a sting in either language. But how can we do this deterministically? We would need a completely different approach.

While that is not a proof that the language is not deterministic, here is one.

Theorem: \(L_1 \cup L_2\) is not a DCFL (because \(a^nb^nc^n\) is not a CFL).

Proof::

\(L = \{a^nb^n: n \ge 1\} \cup \{a^nb^{2n}: n \ge 1\}\)

It is easy to construct a NPDA for \(\{a^nb^n: n\ge 1\}\) and a NPDA for \(\{a^nb^{2n}: n \ge 1\}\). These two can be joined together by a new start state and \(\lambda\)-transitions to create a NPDA for L. Thus, L is CFL.

Now show \(L\) is not a DCFL. Assume that there is a deterministic PDA \(M\) such that \(L = L(M)\). We will construct a PDA that recognizes a language that is not a CFL and derive a contradiction.

Construct a PDA \(M'\) as follows:

Todo

type:	Figure

Show figure

1. Create two copies of \(M: M_1\) and \(M_2\). The same state in \(M_1\) and \(M_2\) are called cousins.

2. Remove accept status from accept states in \(M_1\), remove initial status from initial state in \(M_2\). In our new PDA, we will start in \(M_1\) and accept in \(M_2\).

3. Outgoing arcs from old accept states in \(M_1\), change to end up in the cousin of its destination in \(M_2\). This joins \(M_1\) and \(M_2\) into one PDA. There must be an outgoing arc since you must recognize both \(a^nb^n\) and \(a^nb^{2n}\). After reading \(n\) b's, must accept if no more b's and continue if there are more b's.

4. Modify all transitions that read a b and have their destinations in \(M_2\) to read a c.

This is the construction of our new PDA.

When we read \(a^nb^n\) and end up in an old accept state in \(M_1\), then we will transfer to \(M_2\) and read the rest of \(a^nb^{2n}\). Only the b's in \(M_2\) have been replaced by c's, so the new machine accepts \(a^nb^nc^n\).

The language accepted by our new PDA is \(a^nb^nc^n\). But this is not a CFL. Contradiction! Thus there is no deterministic PDA \(M\) such that \(L(M) = L\). Q.E.D.

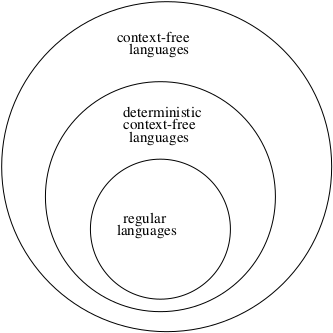
Based on this information, we now can update our model of the Formal Languages Universe.

2. Grammars for Deterministic Context-free Languages¶

Now we know that:

All CFL can be generated by a CFG, and implemented by a NPDA.
Not all CFL can be generated using a DPDA.
So some CFG are associated with only non-deterministic PDAs. Nondeterminism gives us something more in terms of capability.

Why do we care? Because we want to parse efficiently. This means, we want to quickly determine if a given string can be generated from a given grammar. Determinism seems to be a fundamental requirement if we hope to do this.

Think of a PDA as a parsing device. No backtracking requires that we can make a decision at every step on what to do next. This is the same as knowing which grammar production comes next. Clearly this is linear time when the grammar has been simplified (no unit productions), because every derivation step consumes an input character. Well... except for \(\lambda\) productions. But we will see soon that these are not really a problem for linear-time processing.

2.1. Top-down Parsing with Lookahead¶

Start with the start symbol Scan left-to-right through the string. At each step, we want only to follow one rule when we look at the current character. Perhaps we don't see a production for the current character, but instead pop something off the stack (\(\lambda\) production). This is why \(\lambda\) productions are still linear, if we don't put too much on the stack when we process a character.

2.2. S-grammars¶

Recall that an S-grammar has all productions of the form:

\(A \rightarrow ax\)

where \(A \in V\), \(a \in T\), and \(x \in V^*\) AND any pair \((A, a)\) can occur in at most one rule.

Obviously this can be parsed efficiently. But, s-grammars are more restrictive than we want. Lots of useful language constructs cannot be defined using an s-grammar. We want to generalize as much as we can to capture a broader subset of CFLs

2.3. LL(k) Grammars¶

LL means "left-to-right" and "left-most derivation" is constructed. \(k\) means that we can look ahead at most \(k-1\) characters. Every s-grammar is LL, but so are more grammars.

Consider this grammar:

\(S \rightarrow aSb \mid ab\)

This is not an s-grammar. But, this is an LL grammar. By looking at the next two characters, we always know which rule to apply.

If we see \(ab\), then apply \(S \rightarrow ab\).

<< What gets consumed, what goes on the stack? >>

Otherwise, apply \(S \rightarrow aSb\)

<< What gets consumed, what goes on the stack? >>

Consider this grammar:

\(S \rightarrow SS \mid aSb \mid ab\)

This is a useful grammar! It captures nested parentheses. This is not an LL(k) grammar for any \(k\). (Can you see why not?)

Just because the grammar is not LL(k) does not mean that the language might not be deterministic. The reasoning for why this was not LL(k) should help you to see how to fix the grammar.

Consider this grammar: \(S \rightarrow aSbS \mid \lambda\)

This is LL.

Example: Derive \(w = abab\).

\(S \Rightarrow aSbS \Rightarrow abS \Rightarrow abaSbS \Rightarrow ababS \Rightarrow abab\).
When the input next input symbol is \(a\), we must use
\(S \rightarrow aSbS\).
When the input next input symbol is \(b\) or string is
empty, we must use \(S \rightarrow \lambda\).

One last problem: This grammar accepts the empty string. If we don't like that, then there is an easy fix. Just define a new start symbol that avoids the \(\lambda\) production.

\(S_0 \rightarrow aSbS\)

\(S \rightarrow aSbS \mid \lambda\)

OpenDSA Stand-alone Modules

Chapter 0 modules

Deterministic Pushdown Automata¶

1. Deterministic Pushdown Automata¶

2. Grammars for Deterministic Context-free Languages¶

2.1. Top-down Parsing with Lookahead¶

2.2. S-grammars¶

2.3. LL(k) Grammars¶