Pushdown Automata¶
1. Pushdown Automata¶
Recall: A DFA \(=(Q, \Sigma, \delta, q_0, F)\).
In a DFA, the tape is read only, the head moves to the right only. DFAs are limited in power. They recognize regular languages but cannot recognize many other "simple" langages like \(a^nb^n\).
We are now going to give the DFA a stack. This new machine is called a Pushdown Automata (PDA). Obviously it gets this name from its new ability to pushdown and store symbols on the stack. This adds a form of additional memory, letting the machine store and retrieve data from the stack.
The old limitations still apply: The tape is read only, the head moves only to the right.
Recall that we could add the concept of nondeterminism to the DFA. This turned out not to change the set of languages that could be recognized by DFAs. What if we add nondeterminism to the PDA?
Definition: A nondeterministic PDA (NPDA) is defined by \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) where
\(Q\) is a finite set of states\(\Sigma\) is the tape (input) alphabet (a finite set)\(\Gamma\) is the stack alphabet (a finite set)\(q_0\) is the initial state, \(q_0 \in Q\)\(z\) is the start stack symbol (marks the bottom of the stack), \(z \in \Gamma\)\(F \subseteq Q\) is the set of final states.\(\delta : Q \times (\Sigma \cup \{\lambda\}) \times \Gamma \rightarrow\) finite subsets of \(Q \times \Gamma^*\)
Transition function \(\delta\) is a mapping to a finite subset of \(Q \times \Gamma^*\)
1.1. Example of transitions¶
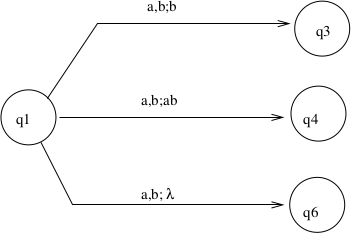
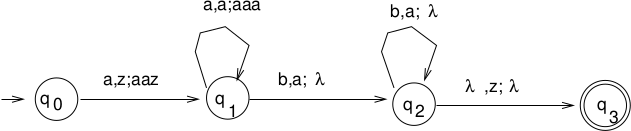
\(\delta(q_1, a, b) = \{(q_3, b),(q_4, ab), (q_6, \lambda)\}\)
Meaning: If in state \(q_1\) with a the current tape symbol and
b the symbol on top of the stack, then pop b, and either
move to \(q_3\) and pushbon stackmove to \(q_4\) and pushabon stack (aon top)move to \(q_6\)
Transitions can be represented using a transition diagram. The diagram for the above transitions is:
Each arc is labeled by a triple \(<x, y; z>\) where \(x\) is the current input symbol, \(y\) is the top of stack symbol which is popped from the stack, and \(z\) is a string that is pushed onto the stack.
Instantaneous Description: \((q, w, u)\)
This is notation to describe the current state of the machine \(q\), unread portion of the input string \(w\), and the current contents of the stack \(u\). (This is a configuration in JFLAP.)
Description of a Move:
Definition: Let \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) be a NPDA. \(L(M) = \{w \in \Sigma^* | (q_0, w, z) \stackrel{*}{\vdash} (p, \lambda, u), p \in F, u \in \Gamma^*\}\). The NPDA accepts all strings that start in \(q_0\) and end in a final state.
NOTE: Stack contents are irrelevant if it ends the string in a final state.
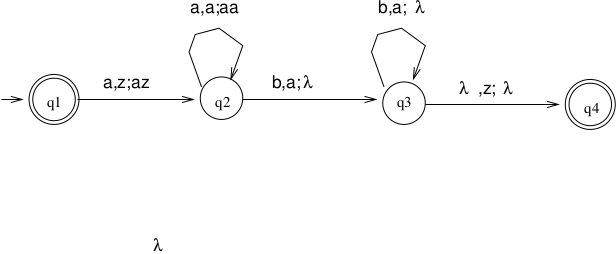
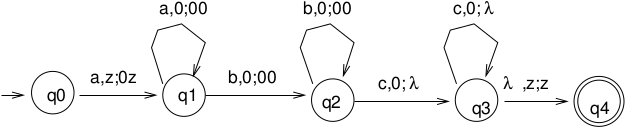
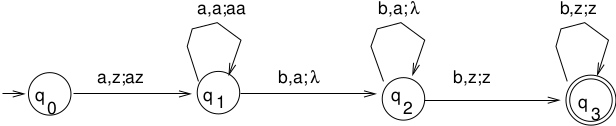
Example 1
\(L = \{a^nb^n | n \ge 0\}, \Sigma = \{a, b\}, \Gamma = \{z,a\}\)
Trace aaabbb
Another Definition for Language Acceptance: NPDA \(M\) accepts \(L(M)\) by empty stack:
\(L(M) = \{w \in \Sigma^* | (q_0, w, z) \stackrel{*}{\vdash} (p, \lambda, \lambda)\}\)
NOTE: 3-tuples above are configurations. Moving from one to another.
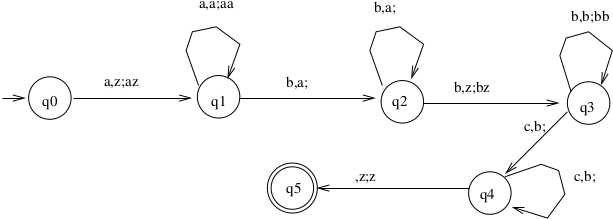
Example 2
\(L = \{a^nb^mc^{n+m} | n,m > 0\}, \Sigma = \{a, b, c\}, \Gamma =\{0, z\}\)
Note: What is the smallest length string that is accepted?
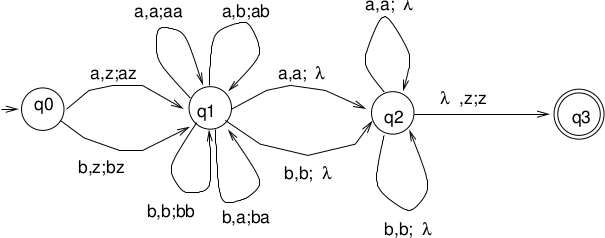
Example 3
\(L = \{ww^R | w \in \Sigma^+ \}, \Sigma = \{a, b\}, \Gamma = ?\)
Trace abbbba
Example 4
\(L = \{ww | w \in \Sigma^*\}, \Sigma =\{a, b\}, \Gamma = ?\)
L is not a CFL, so there is no NPDA!
Examples for you to try on your own: (solutions are at the end of this section).
- \(L = \{a^nb^m | m > n, m, n > 0\}, \Sigma = \{a, b\}, \Gamma = \{z, a\}\)
- \(L = \{a^nb^{n+m}c^m | n, m> 0\}, \Sigma=\{a, b, c\}\)
- \(L = \{a^nb^{2n} | n > 0\}, \Sigma=\{a,b\}\)
Reminder: The acceptance definition is that we accept if we end in a final state. The contents of the stack are irrelevent.
Definition: A PDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) is deterministic if for every \(q \in Q, a \in \Sigma \cup \{\lambda\}, b \in \Gamma\)
- \(\delta(q, a, b)\) contains at most 1 element
- if \(\delta(q, \lambda, b) \neq \emptyset\) then \(\delta(q, c, b) = \emptyset\) for all \(c \in \Sigma\).
Definition: \(L\) is DCFL iff \(\exists\) DPDA \(M\) such that \(L = L(M)\).
Examples:
- Previous PDA for \(\{a^nb^n | n\ge 0\}\) is deterministic.
- Previous PDA for \(\{a^nb^mc^{n+m} | n, m> 0\}\) is probably deterministic
- Previous PDA for \(\{ww^R | w \in \Sigma^+\}, \Sigma = \{a, b\}\) is nondeterministic.
Example 5
\(L = \{a^nb^m | m > n, m, n > 0\}, \Sigma =\{a, b\}, \Gamma = \{z, a\}\)
Example 6
\(L = \{a^nb^{n+m}c^m | n, m > 0\}, \Sigma = \{a, b, c\}\)
Example 7
\(L = \{a^nb^{2n} | n > 0\}, \Sigma=\{a, b\}\)
1.2. Equivalence of Acceptance Definitions¶
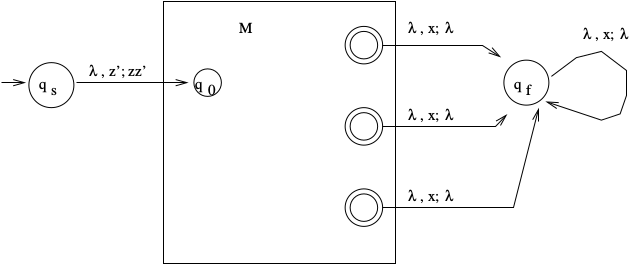
Theorem Given NPDA M that accepts by final state, \(\exists\) NPDA \(M'\) that accepts by empty stack such that \(L(M) = L(M')\).
Proof (sketch)
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)Construct \(M' = (Q', \Sigma, {\Gamma}^{'}, {\delta}^{'}, q_s, z', F')\) (NOTE: \(z'\) is a new symbol)\(Q' = Q \cup \{q_s, q_f\}\)\({\Gamma}^{'} = \Gamma \cup \{z'\}\) (NOTE: \(z' \not\in \Gamma\), never popped in old machine)\(q_s\) is new start state.\(F = \{\}\). Irrelevant. The only time the stack will be empty is in \(q_f\).
Here, \(x\) is any symbol in \({\Gamma}^{'}\). (\(l\) represents \(\lambda\)).Don't really need the concept of a final state in this case. QED.
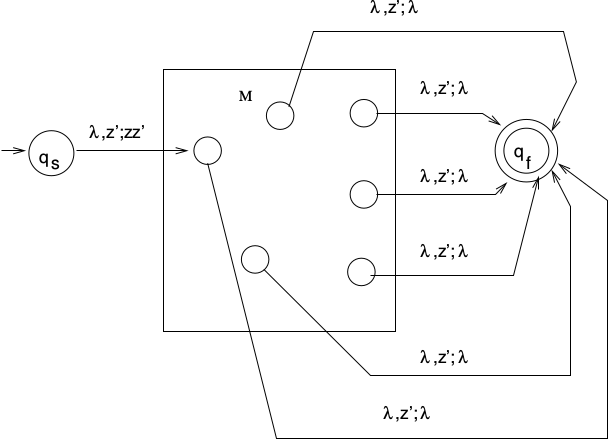
Theorem: Given NPDA \(M\) that accepts by empty stack, \(\exists\) NPDA \(M'\) that accepts by final state.
Proof:
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)Construct \(M' = (Q', \Sigma, \Gamma^{'}, \delta^{'}, q_s, z', F')\)\(Q' = Q \cup \{q_s, q_f\}\)\(\Gamma^{'} = \Gamma \cup \{z'\}\)\(q_s\) is new start state.\(F^ = \{q_f\}\). The only time the stack will be empty is in \(q_f\).\((q_f, z') \in \delta(q, \lambda, z')\) for all \(q \in Q\).
If \(M\) accepted in some state, then that means the stack was empty. In \(M'\), at the same state, the stack will contain only \(z'\), and the new transition can be followed to \(q_f\). QED
