Transforming Grammars¶

1. Transforming Grammars¶

We use grammars to represent a programming language. Want to know: Is a given string (or program \(x\)) valid (syntactically correct)? Same as asking if it is in the language.

Last time we showed that if we could transform a CFG into a CFG with no \(\lambda\)-productions, and no rules like \(A \rightarrow B\), then we could determine if \(w\) is in or not in \(L(G)\) in \(2|w|\) rounds, each step adding a terminal or increasing in length. (Linz 5.2)

This works, but it is not fast, that is, not linear!

We will look at lots of methods for transforming grammars. Some will be forms that are easier to work with, some are easier to use in proofs.

Key question: Are there ways to transform (restrict) CFGs such that

1) We can process efficiently

2) without restricting the power of CFGs

Note

Ask yourself: What does it mean "without restricting the power of CFGs"?

Specifically, we will look at restrictions on the right hand side of the production rules. We want to be able to automatically transform an arbitrary CFG into an equivalent restricted CFG.

We will consider CFL without \(\lambda\). It would be easy to add \(\lambda\) to any grammar by adding a new start symbol \(S_0\),

\(S_0 \rightarrow S \mid \lambda\)

Substitution Theorem Let \(G\) be a CFG. Suppose \(G\) contains

\(A \rightarrow x_1Bx_2\)

where \(x_i \in (V \cup T)^{*}\), \(A\) and \(B\) are different variables, and \(B\) has the productions

\(B \rightarrow y_1|y_2|\ldots|y_n\).

Then, we can construct \(G'\) from \(G\) by deleting

\(A \rightarrow x_1Bx_2\)

from \(P\) and adding to it

\(A \rightarrow x_1y_1x_2|x_1y_2x_2|\ldots | x_1y_nx_2\).

Then, \(L(G) = L(G')\).

Question: Why don't we also delete \(B\) rules?

Answer: These might be used by another production

Question: What if \(A\) and \(B\) are the same?

\[\begin{split}\begin{array}{lll} S \rightarrow aBa & \mbox{becomes} & S \rightarrow aaSa \mid aaa\\ B \rightarrow aS \mid a & & B \rightarrow aS \mid a\\ \end{array}\end{split}\]

Then the B productions become useless productions.

Definition: A production of the form \(A \rightarrow Ax\), \(A \in V, x \in (V \cup T)^*\) is left recursive.

Example: Previous expression grammar was left recursive. (from Chapter 5 notes)

It is left recursive because it has SOME left recursive productions. Not all of the productions are left recursive.

\(E \rightarrow E+T \mid T\)

\(T \rightarrow T*F \mid F\)

\(F \rightarrow I \mid (E)\)

\(I \rightarrow a \mid b\)

A top-down parser (like LL parsing) would want to derive the leftmost terminal as soon as possible. But in the left recursive grammar above, in order to derive a sentential form that has the leftmost terminal, we have to derive a sentential form that has other terminals in it.

Derivation of \(a+b+a+a\) is:

\[E \Rightarrow E+T \Rightarrow E+T+T \Rightarrow E+T+T+T \stackrel{*}{\Rightarrow} a+T+T+T\]

NOTE: nicer to have a grammar that would derive the \(a\) first without all the other +'s.

We will eliminate the left recursion so that we can derive a sentential form with the leftmost terminal and no other terminals.

Theorem (Removing Left recursion) Let \(G = (V,T,S,P)\) be a CFG. Divide productions for variable \(A\) into left-recursive and non left-recursive productions:

\(A \rightarrow Ax_1 \mid Ax_2 \mid \ldots \mid Ax_n\)

\(A \rightarrow y_1 \mid y_2 \mid \ldots \mid y_m\)

where \(x_i\), \(y_i\) are in \((V \cup T)^*\).

Any derivation will start with \(y_i\).

\(A\) is not a prefix of any of the second type.

Then \(G = (V \cup \{Z\}, T, S, P')\) and \(P'\) replaces rules of form above by

\(A \rightarrow y_i \mid y_iZ, i = 1, 2, \ldots, m\)

\(Z \rightarrow x_i \mid x_iZ, i = 1, 2, \ldots, n\)

Note

Consider a derivation: \(y_3x_7x_1x_3\)

Example 1

\[\begin{split}\begin{array}{lll} E \rightarrow E+T \mid T & \mbox{becomes} & E \rightarrow T \mid TZ\\ & & Z \rightarrow +T \mid +TZ \\ T \rightarrow T*F \mid F & \mbox{becomes} & T \rightarrow F \mid FY \\ & & Y \rightarrow *F \mid *FY \\ \end{array}\end{split}\]

When you get rid of left-recursion, the grammar is in the appropriate form for a top-down parser, but the grammar has more variables and productions.

Now, the derivation of \(a+b+a+a\) is:

\(E \Rightarrow TZ \Rightarrow FZ \Rightarrow IZ \Rightarrow aZ\)

Didn't have to look at any other terminals yet!

Useless productions

\(S \rightarrow aB \mid bA\)

\(A \rightarrow aA\)

\(B \rightarrow Sa\)

\(C \rightarrow cBc \mid a\)

What can you say about this grammar?

\(A\), \(S\), and \(B\) are useless variables since they can't derive a string of terminals. \(C\) is useless because you can't get \(S \stackrel{*}{\Rightarrow} xCy \stackrel{*}{\Rightarrow} w\), where \(w \in T^*\).

Theorem: (useless productions) Let \(G\) be a CFG. Then \(\exists\ G'\) that does not contain any useless variables or productions such that \(L(G) = L(G')\).

To Remove Useless Productions:

Let \(G = (V,T,S,P)\).

I. Compute \(V_1 =\) {Variables that can derive strings of terminals}

1. \(V_1 = \emptyset\)

2. Repeat until no more variables added

* For every \(A \in V\) with \(A \rightarrow x_1x_2\ldots x_n\), \(x_i \in (T^* \cup V_1)\), add \(A\) to \(V_1\)

3. \(P_1 =\) all productions in \(P\) with symbols in \((V_1 \cup T)*\)

Then \(G_1 = (V_1, T, S, P_1)\) has no variables that can't derive strings.

Now we need to get rid of productions we can't use.

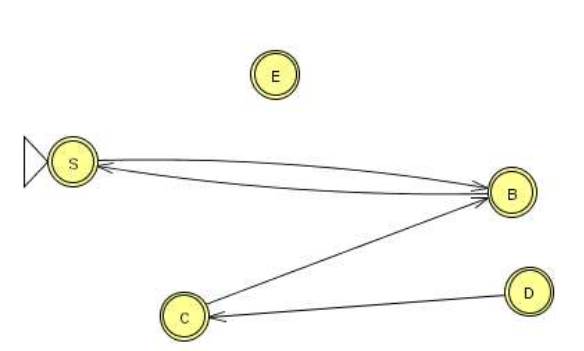
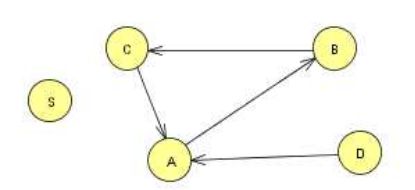
Draw Variable Dependency Graph

For \(A \rightarrow xBy\), draw \(A \rightarrow B\).

Draw \(A\) in a circle, \(B\) in a circle, and an arc from \(A\) to \(B\).

Remove productions for \(V\) if there is no path from \(S\) to \(V\) in the dependency graph. Resulting Grammar \(G'\) is such that \(L(G) = L(G')\) and \(G'\) has no useless productions.

Example 2

\(S \rightarrow aB \mid bA\)
\(A \rightarrow aA\)
\(B \rightarrow Sa \mid b\)
\(C \rightarrow cBc \mid a\)
\(D \rightarrow bCb\)
\(E \rightarrow Aa \mid b\)

\(V_1 = \{B, C, D, E, S\}\), \(A\) is useless.

\[\begin{split}\begin{array}{ll} G_1: \ \ \ \ & S \rightarrow aB \\ & B \rightarrow Sa \mid a \\ & C \rightarrow cBc \mid a \\ \end{array}\end{split}\]

Dependency graph:

\[\begin{split}\begin{array}{ll} G': \ \ \ \ & S \rightarrow aB \\ & B \rightarrow Sa \mid b \\ \end{array}\end{split}\]

Q: How would you implement II? How do you know which nodes are accessible from S? Use DFS or BFS.

NOTE: Last time talked about simpler CFG that had no \(\lambda\)-productions, now we will show how to get rid of them.

Theorem (remove \(\lambda\) productions) Let \(G\) be a CFG with \(\lambda\) not in \(L(G)\). Then \(\exists\) a CFG \(G'\) having no \(\lambda\)-productions such that \(L(G) = L(G')\).

To Remove \(\lambda\) -productions

1. Let \(V_n = \{A \mid \exists\ \mbox{production}\ A \rightarrow \lambda\}\)

2. Repeat until no more additions

* if \(B \rightarrow A_1A_2 \ldots A_m\) and \(A_i \in V_n\) for all \(i\), then put \(B\) in \(V_n\)

THUS, \(V_n = \{A \mid A\stackrel{*}{\Rightarrow} \lambda \}\)

3. Construct \(G'\) with productions \(P'\) such that

* If \(A \rightarrow x_1x_2\ldots x_m \in P, m \ge 1\), then put all productions formed when \(x_j\) is replaced by \(\lambda\) (for all \(x_j \in V_n\)) such that \(|\mbox{rhs}| \ge 1\) into \(P'\).

Example 3

\(S \rightarrow Ab\)
\(A \rightarrow BCB \mid Aa\)
\(B \rightarrow b \mid \lambda\)
\(C \rightarrow cC \mid \lambda\)

\(V_n = \{B, C, A\}\)

\[\begin{split}\begin{array}{ll} G': \ \ \ \ \ & S \rightarrow Ab \mid b\\ &A \rightarrow BCB \mid BC \mid BB \mid CB \mid B \mid C \mid Aa \mid a\\ &B \rightarrow b \\ &C \rightarrow cC \mid c \\ \end{array}\end{split}\]

NOTE: Don't add \(A \rightarrow \lambda\)!

Definition: Unit Production

\(A \rightarrow B\)

where \(A, B \in V\).

Consider removing unit productions:

Suppose we have

\[\begin{split}\begin{array}{lll} A \rightarrow B & \ \ \ \ \ \mbox{becomes} \ \ \ \ \ & A \rightarrow a \mid ab \\ B \rightarrow a \mid ab \\ \end{array}\end{split}\]

But what if we have

\[\begin{split}\begin{array}{lll} A \rightarrow B & \ \ \ \ \ \mbox{becomes} \ \ \ \ \ & A \rightarrow C \\ B \rightarrow C & & B \rightarrow A \\ C \rightarrow A & & C \rightarrow B \\ \end{array}\end{split}\]

But we don't get rid of unit-productions!

Theorem (Remove unit productions) Let \(G = (V, T, S, P)\) be a CFG without \(\lambda\)-productions. Then \(\exists\) CFG \(G = (V', T', S, P')\) that does not have any unit-productions and \(L(G) = L(G')\).

To Remove Unit Productions:

1. Find for each \(A\), all \(B\) such that \(A \stackrel{*}{\Rightarrow} B\)

(Draw a dependency graph howing relationship of Unit productions. Just draw arc for each \(A \rightarrow B\) rule.

Draw \(A\) in a circle, \(B\) in a circle, and an arc from \(A\) to \(B\).)

2. Construct \(G' = (V', T', S, P')\) by

(a) Put all non-unit productions in \(P'\)

(b) For all \(A \stackrel{*}{\Rightarrow} B\) such that \(B \rightarrow y_1 \mid y_2 \mid \ldots y_n \in P'\), put \(A \rightarrow y_1 \mid y_2 \mid \ldots y_n \in P'\)

Run DFS with \(A\) as root.

Note the star in \(A \stackrel{*}{\Rightarrow} B\)

Never put a unit production in \(P'\).

Example 4

\(S \rightarrow AB\)
\(A \rightarrow B\)
\(B \rightarrow C \mid Bb\)
\(C \rightarrow A \mid c \mid Da\)
\(D \rightarrow A\)

\[\begin{split}\begin{array}{ll} \mbox{After a)} & S \rightarrow AB \\ & B \rightarrow Bb \\ & C \rightarrow c \mid Da \\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{ll} G': & S \rightarrow AB \\ & A \rightarrow Bb \mid c \mid Da \\ & B \rightarrow Bb \mid c \mid Da\\ & C \rightarrow c \mid Bb \mid Da\\ & D \rightarrow c \mid Bb \mid Da\\ \end{array}\end{split}\]

Theorem: Let \(L\) be a CFL that does not contain \(\lambda\). Then \(\exists\) a CFG for \(L\) that does not have any useless productions, \(\lambda\)-productions, or unit-productions.

Proof:

1. Remove \(\lambda\)-productions

2. Remove unit-productions

3. Remove useless productions

Note order is very important. Removing \(\lambda\)-productions can create unit-productions! QED.

There are additional examples in the book.

Definition: A CFG is in Chomsky Normal Form (CNF) if all productions are of the form

\(A \rightarrow BC \ \ or A \rightarrow a\)

where \(A, B, C \in V\) and \(a \in T\).

Why would you want to put a grammar in this form? Because it is easier to work with in proofs.

Theorem 1 :

Any CFG \(G\) with \(\lambda\) not in \(L(G)\) has an equivalent grammar in CNF.

Proof:

1. Remove \(\lambda\)-productions, unit productions, and useless productions.

2. For every right-hand-side of length \(> 1\), replace each terminal \(x_i\) by a new variable \(C_j\) and add the production \(C_j \rightarrow x_i\).

Note: All productions are in the correct form or the right-hand-side is a string of variables.

3. Replace every right-hand-side of length \(> 2\) by a series of productions, each with right-hand-side of length 2. QED.

Example 5

\(S \rightarrow CBcd\)
\(B \rightarrow b\)
\(C \rightarrow Cc \mid e\)

\[\begin{split}\begin{array}{lll} \mbox{(after step 1)} & G': & S \rightarrow CBC_1C_2 \\ && B \rightarrow b \\ && C \rightarrow CC_3 \mid e \\ && C_1 \rightarrow c \\ && C_2 \rightarrow d \\ && C_3 \rightarrow c \\ \\ \mbox{(after step 2)} & G'': & S \rightarrow CZ_1 \\ && Z_1 \rightarrow BZ_2 \\ && Z_2 \rightarrow C_1C_2 \\ && B \rightarrow b \\ && C \rightarrow CC_3 \mid e \\ && C_1 \rightarrow c \\ && C_2 \rightarrow d \\ && C_3 \rightarrow c \\ \end{array}\end{split}\]

NOTE: Can get rid of \(\lambda\)-productions and unit productions first!

Definition: A CFG is in Greibach normal form (GNF) if all productions have the form

\(A \rightarrow ax\)

where \(a \in T\) and \(x \in V^*\)

This is like an s-grammar (or simple grammar, p.142 Linz), except the s-grammar definition includes a further restriction that any pair \((A, a)\) can occur at most in one rule.

This is so that you wouldn't have to backtrack (only one choice to match the derivation of a string). So it very restrictive.

Theorem 2

For every CFG \(G\) with \(\lambda\) not in \(L(G)\), \(\exists\) a grammar in GNF.

Proof:

1. Rewrite grammar in CNF.

2. Relabel Variables \(A_1, A_2, \ldots A_n\)

3. Eliminate left recursion and use substitution to get all productions into the form:

\(A_i \rightarrow A_jx_j, j > i\)

\(Z_i \rightarrow A_jx_j, j \le n\)

\(A_i \rightarrow ax_i\)

where \(a \in T, x_i \in V*\), and \(Z_i\) are new variables introduced for left recursion.

Use Theorems 6.1 and 6.2 to get rid of left recursion.

4. All productions with \(A_n\) are in the correct form, \(A_n \rightarrow ax_n\). Use these productions as substitutions to get \(A_{n-1}\) productions in the correct form. Repeat with \(A_{n-2}\), \(A_{n-3}\), etc until all productions are in the correct form.

WHAT YOU SHOULD KNOW: know forms, GNF, CNF, unit production, left recursion, etc. Do not need to memorize rules for transforming, but should understand how to do it.

OpenDSA Stand-alone Modules

Chapter 0 modules

Transforming Grammars¶

1. Transforming Grammars¶