Minimizing the Number of States in a DFA¶
1. Minimizing the Number of States in a DFA¶
Why do we need to do this?
If you have an NFA with \(n\) states, what is the maximum number of states in the equivalent DFA created? \(2^n\)
Algorithm
Identify states that are indistinguishable
- These states form a new state
Definition: Two states \(p\) and \(q\) are indistinquishable if for all \(w \in \Sigma^*\)
Definition: Two states \(p\) and \(q\) are distinquishable if \(\exists w \in \Sigma^*\) such that
\(p\) and \(q\) appear to be different.
All that an acceptor cares about is accepting or rejecting strings.
Select any pair of states, \(p\) and \(q\).
- If, in either case, we accept/reject the exact same set set of strings, then there is no difference between them.
- So, we can combine them.
- Remember the definition for \(\delta^*(p, w)\). Look at things this way: It is telling us that we don't care about the prior history before we got to the current state with whatever remains of the input.
Distinguishability is an equivalence relation.
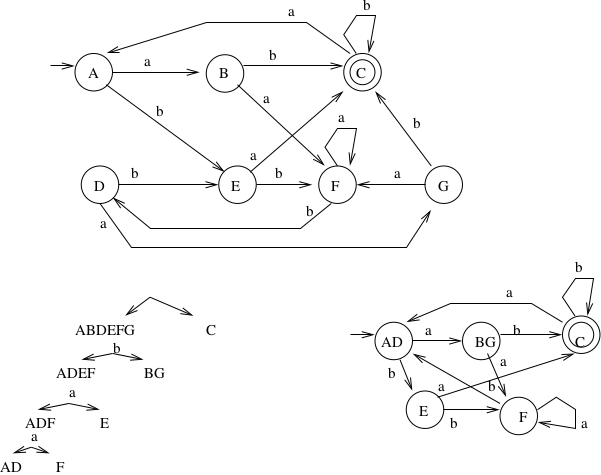
Example:
Look at A on \(a\), \(ab\):
- \(a\) goes to a non-final state, \(ab\) goes to a final state
Look at F on \(a\), \(ab\):
- \(a\) goes to a non-final state, \(ab\) goes to a non-final state
Look at D on \(a\), \(ab\):
- \(a\) goes to a non-final state, \(ab\) goes to a final state
So, we know that F must be in a different equivalence subset than A and D. A and D might or might not end up being equivalent.
Example
Figure 1: Minimization 1
The first step will always split the states into the subset of non-final vs. the subset of final states. In the tree, each step after that corresponds to testing the given character against the states in that subset to see if they all go to the same subset. Split them up when they do not go to the same place.
Todo
| type: | Slideshow |
|---|
Replace the images above with a slideshow that presents, step-by-step, the process of minimizing the DFA.
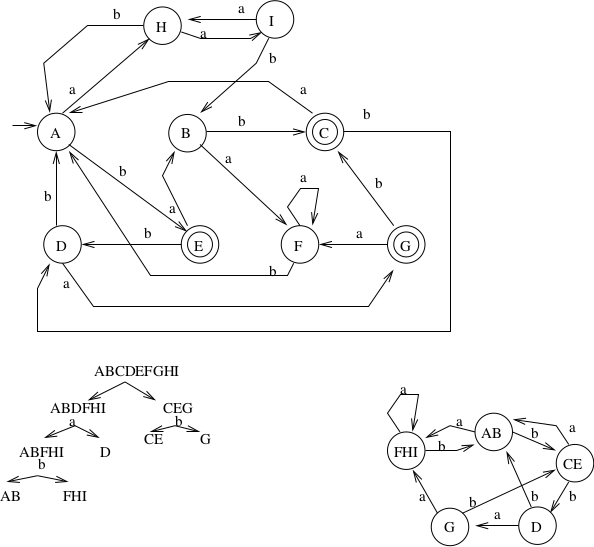
Example:
Figure 2: Minimization 2
