Non-Deterministic Finite Automata¶
1. NFA: Non-Deterministic Finite Automata¶
Definition:
Define a NFA as \((Q, \Sigma, \delta, q_0, F)\) where
- \(Q\) is a finite set of states
- \(\Sigma\) is the input alphabet (a finite set)
- \(q_0\) is the initial state (\(q_0 \in Q\))
- \(F \subseteq Q\) is a set of final states
- \(\delta: Q \times(\Sigma \cup \{\lambda\}) \rightarrow 2^Q\) (\(2^Q\) here means the power set of \(Q\))
The specific difference from a DFA is that, while the result of \(\delta\) for the DFA is some state \(q \in Q\), the result of \(\delta\) for the NFA is any subset of \(Q\).
Non-deterministic means that it allows choices. From a state on input \(b\), \(\delta\) might include transitions to more than one state.
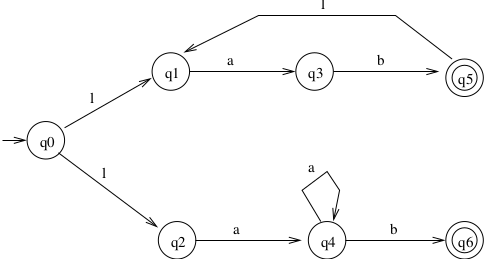
Example:
Figure 1: Example of NFA
In this example, \(\delta(q_0, a) = \{q_1, q_2\}\). (So, \(\delta\) is no longer meets the mathematical definition of a function!)
Hopefully this one is easy to understand: We two disjoint paths, effectively giving us the union of two languages: \(L = \{aa\} \cup \{ab^nb \mid n \ge 0\}\).
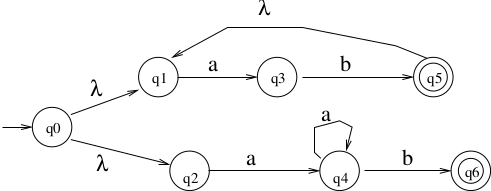
Example:
\(L = \{(ab)^n \mid n>0\} \cup \{a^nb \mid n>0\}\).
Figure 2: Second Example of NFA A simple "go this way or go the other way".
Definition: \(q_j \in {\delta}^{*}(q_i,w)\) if and only if there exists some walk from \(q_i\) to \(q_j\) labeled \(w\).
From previous example:
\(\delta^{*}(q_0, ab) = \{q_5, q_6, q_1\}\).
\(\delta^{*}(q_0, aba) = \{q_3\}\).
Definition: For an NFA \(M\), \(L(M)= \{w \in {\Sigma}^{*} \mid \delta^{*}(q_0,w) \cap F \neq \emptyset \}\)
What does this mean? It means that the machine accepts all strings \(w\) from the set of all possible strings (generated from the alphabet \(\Sigma\)) such that the states reachable on \(w\) from the start state (\(q_0\)) is in the final state set.
Note that it does not matter that there are paths where \(w\) can go wrong. What matters is that there is at least one way for \(w\) to be right.
Why nondeterminism? It makes it easier to describe a FA. What does "easier" mean? It could mean easier to comprehend when looking at it. Or maybe easier for the developer to write it. Or maybe smaller (in terms of the number of states). Or maybe it is more efficient (but probably not because non-determinism can be expensive to simulate). From a performance point of view, to determine if a string is accepted can take a LONG time to try out all possibilities. But, all that we care about right now is existance, not performance.
2. NFA vs. DFA: Which is more powerful?¶
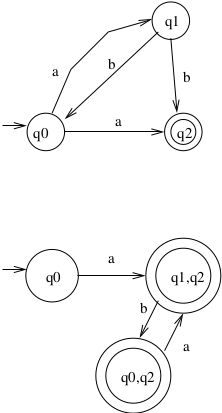
Consider the following NFA. Can this NFA be converted to a DFA?
Figure 3: An NFA and equivalent DFA
Note
Try this out using JFLAP. JFLAP can convert a NFA to a DFA.
Theorem 1 and Proof
Theorem: Given an NFA \(M_N = (Q_N, \Sigma, \delta_N, q_0, F_N)\), there exists a DFA \(M_D = (Q_D, \Sigma, \delta_D, q_0, F_D)\) such that \(L(M_N) = L(M_D)\).
Proof: We can use an algorithm to convert \(M_N\) to \(M_D\).
\(Q_D = 2^{Q_N}\)
\(F_D = \{Q\in Q_D \mid \exists q_i \in Q \mathrm{with} q_i \in F_N \}\)
Interpretation: A state \(q_D\) in \(M_D\) is final if any of the states from \(M_N\) in the subset that \(q_D\) corresponds to is final.
\(\delta_D : Q_D \times \Sigma \rightarrow Q_D\)
Algorithm to construct \(M_D\)
Start state is \(\{q_0\} \cup \mathrm{closure}(q_0)\) (Note that "closure" of \(q_0\) is a set of states defined as \(q_0\) plus all states reachable from \(q_0\) by \(\lambda\) transitions.
While can add an edge (that is, while missing a transition from \(\delta_D\))
- Choose a state \(A = \{q_i, q_j, ..., q_k\}\) with missing edge for \(a \in \Sigma\)
- Compute \(B = \delta^{*}(q_i, a) \cup \delta^{*}(q_j, a) \cup \ldots \cup \delta^{*}(q_k, a)\)
- Add state \(B\) if it doesn't exist
- Add edge from \(A\) to \(B\) with label \(a\)
Identify final states.
For a state in \(Q_D\), if any of its base \(Q_N\) states are final, then it is final.
If \(\lambda \in L(M_N)\), then make the start state final.
Intuition: Given a state in \(M_N\) and a character, you can get to some subset of the states in \(M_N\). Consider that to be a state in \(M_D\). There are only so many subsets of the set of \(M_N\) states: That would be members of the powerset of \(M_D\) states.
Example:
Figure 4: Another NFA to convert
Let's begin with the start state. Closure(\(q_0\)) in \(M_N\) is \(\{q_0, q_1, q_2\}\). So this is the start state.
For example: From \(M_D\) state \(q_0,q_1,q_2\), determine the subset of states that can be reached from any of those states on letter \(a\). This would be the subset \(q_3,q_4\).
Note
Do this conversion using JFLAP. You should get the following result.
Answer:
Figure 5: Converted DFA
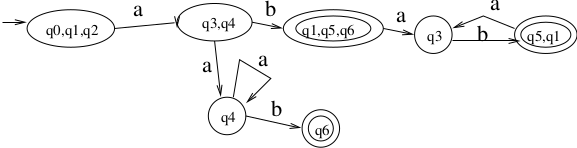
Todo
| type: | Slideshow |
|---|
Replace the images above with a slideshow that presents first the NFA, and then shows, step-by-step, the process of building the DFA.
Conclusion: NFA adds no new capability. So why bother with the idea?
- First, it wasn't obvious that they are the same. NFA is a useful concept.
- NFA tend to be "smaller" and "simpler" than the equivalent DFA. (At least morphologically, but perhaps the language of a NFA is hard to grasp.)
- We will see times when it is easier to see a conversion from something to a NFA, and we know that this can always be converted in turn to a DFA.
