33.2. Reductions¶
33.2.1. Reductions¶
This module introduces an important concept for understanding the relationships between problems, called reduction. Reduction allows us to solve one problem in terms of another. Equally importantly, when we wish to understand the difficulty of a problem, reduction allows us to make relative statements about upper and lower bounds on the cost of a problem (as opposed to an algorithm or program).
Because the concept of a problem is discussed extensively in this chapter, we want notation to simplify problem descriptions. Throughout this chapter, a problem will be defined in terms of a mapping between inputs and outputs, and the name of the problem will be given in all capital letters. Thus, a complete definition of the sorting problem could appear as follows:
SORTING
Input: A sequence of integers x0,x1,x2,…,xn−1.
Output: A permutation y0,y1,y2,…,yn−1 of the sequence such that yi≤yj whenever i<j.
When you buy or write a program to solve one problem, such as sorting, you might be able to use it to help solve a different problem. This is known in software engineering as software reuse. To illustrate this, let us consider another problem.
PAIRING
Input: Two sequences of integers X=(x0,x1,...,xn−1) and Y=(y0,y1,...,yn−1).
Output: A pairing of the elements in the two sequences such that the least value in X is paired with the least value in Y, the next least value in X is paired with the next least value in Y, and so on.
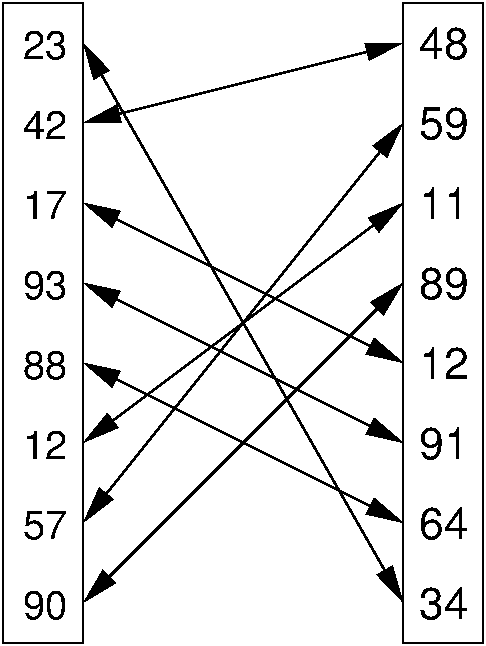
Figure 33.2.1: An illustration of PAIRING. The two lists of numbers are paired up so that the least values from each list make a pair, the next smallest values from each list make a pair, and so on.
Figure 33.2.1 illustrates PAIRING. One way to solve PAIRING is to use an existing sorting program to sort each of the two sequences, and then pair off items based on their position in sorted order. Technically we say that in this solution, PAIRING is reduced to SORTING, because SORTING is used to solve PAIRING.
Notice that reduction is a three-step process. The first step is to convert an instance of PAIRING into two instances of SORTING. The conversion step in this example is not very interesting; it simply takes each sequence and assigns it to an array to be passed to SORTING. The second step is to sort the two arrays (i.e., apply SORTING to each array). The third step is to convert the output of SORTING to the output for PAIRING. This is done by pairing the first elements in the sorted arrays, the second elements, and so on.
A reduction of PAIRING to SORTING helps to establish an upper bound on the cost of PAIRING. In terms of asymptotic notation, assuming that we can find one method to convert the inputs to PAIRING into inputs to SORTING "fast enough", and a second method to convert the result of SORTING back to the correct result for PAIRING "fast enough", then the asymptotic cost of PAIRING cannot be more than the cost of SORTING. In this case, there is little work to be done to convert from PAIRING to SORTING, or to convert the answer from SORTING back to the answer for PAIRING, so the dominant cost of this solution is performing the sort operation. Thus, an upper bound for PAIRING is in O(nlogn).
It is important to note that the pairing problem does not require that elements of the two sequences be sorted. This is merely one possible way to solve the problem. PAIRING only requires that the elements of the sequences be paired correctly. Perhaps there is another way to do it? Certainly if we use sorting to solve PAIRING, the algorithms will require Ω(nlogn) time. But, another approach might conceivably be faster.
There is another use of reductions aside from applying an old algorithm to solve a new problem (and thereby establishing an upper bound for the new problem). That is to prove a lower bound on the cost of a new problem by showing that it could be used as a solution for an old problem with a known lower bound.
Assume we can go the other way and convert SORTING to PAIRING "fast enough". What does this say about the minimum cost of PAIRING? We know that the lower bound for SORTING in the worst and average cases is in Ω(nlogn). In other words, the best possible algorithm for sorting requires at least nlogn time.
Assume that PAIRING could be done in O(n) time. Then, one way to create a sorting algorithm would be to convert SORTING into PAIRING, run the algorithm for PAIRING, and finally convert the answer back to the answer for SORTING. Provided that we can convert SORTING to/from PAIRING "fast enough", this process would yield an O(n) algorithm for sorting! Because this contradicts what we know about the lower bound for SORTING, and the only flaw in the reasoning is the initial assumption that PAIRING can be done in O(n) time, we can conclude that there is no O(n) time algorithm for PAIRING. This reduction process tells us that PAIRING must be at least as expensive as SORTING and so must itself have a lower bound in Ω(nlogn).
To complete this proof regarding the lower bound for PAIRING, we need now to find a way to reduce SORTING to PAIRING. This is easily done. Take an instance of SORTING (i.e., an array A of n elements). A second array B is generated that simply stores i in position i for 0≤i<n. Pass the two arrays to PAIRING. Take the resulting set of pairs, and use the value from the B half of the pair to tell which position in the sorted array the A half should take; that is, we can now reorder the records in the A array using the corresponding value in the B array as the sort key and running a simple Θ(n) Binsort. The conversion of SORTING to PAIRING can be done in O(n) time, and likewise the conversion of the output of PAIRING can be converted to the correct output for SORTING in O(n) time. Thus, the cost of this "sorting algorithm" is dominated by the cost for PAIRING.
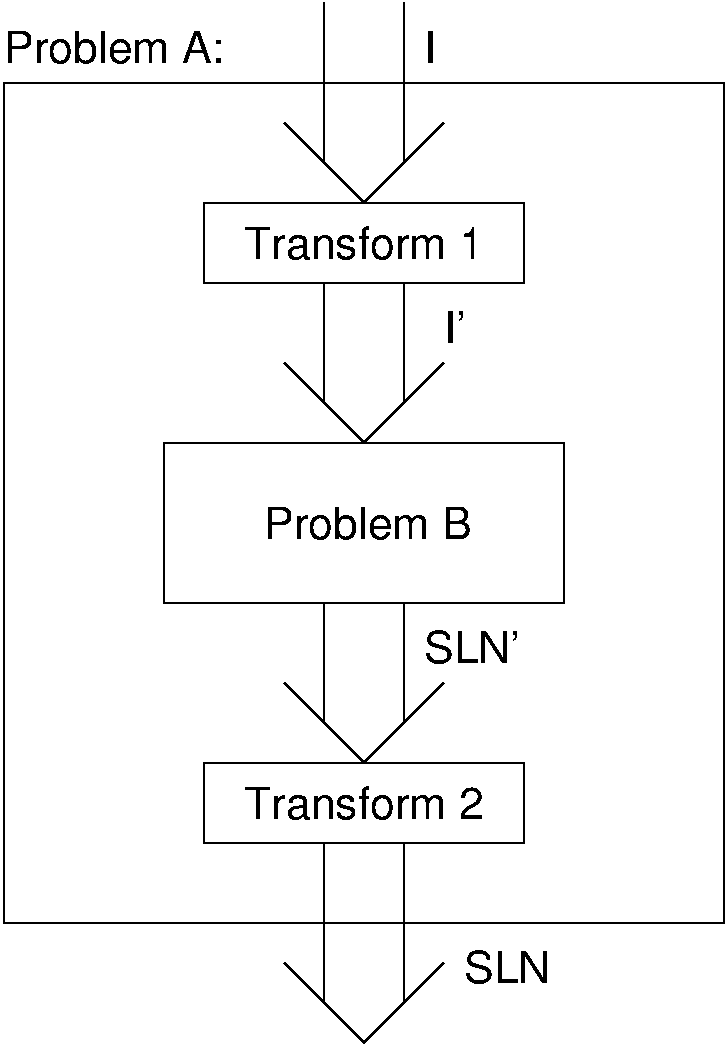
Consider any two problems for which a suitable reduction from one to the other can be found. The first problem takes an arbitrary instance of its input, which we will call I, and transforms I to a solution, which we will call SLN. The second problem takes an arbitrary instance of its input, which we will call I', and transforms I' to a solution, which we will call SLN'. We can define reduction more formally as a three-step process:
- Transform an arbitrary instance of the first problem to an instance of the second problem. In other words, there must be a transformation from any instance I of the first problem to an instance I' of the second problem.
- Apply an algorithm for the second problem to the instance I', yielding a solution SLN'.
- Transform SLN' to the solution of I, known as SLN. Note that SLN must in fact be the correct solution for I for the reduction to be acceptable.
Figure 33.2.2 shows a graphical representation of the general reduction process, showing the role of the two problems, and the two transformations. Next is a slideshow that shows the steps for the reduction of SORTING to PAIRING.
It is important to note that the reduction process does not give us an algorithm for solving either problem by itself. It merely gives us a method for solving the first problem given that we already have a solution to the second. More importantly for the topics to be discussed in the remainder of this chapter, reduction gives us a way to understand the bounds of one problem in terms of another. Specifically, given efficient transformations, the upper bound of the first problem is at most the upper bound of the second. Conversely, the lower bound of the second problem is at least the lower bound of the first.
As a second example of reduction, consider the simple problem of multiplying two n-digit numbers. The standard long-hand method for multiplication is to multiply the last digit of the first number by the second number (taking Θ(n) time), multiply the second digit of the first number by the second number (again taking Θ(n) time), and so on for each of the n digits of the first number. Finally, the intermediate results are added together. Note that adding two numbers of length M and N can easily be done in Θ(M+N) time. Because each digit of the first number is multiplied against each digit of the second, this algorithm requires Θ(n2) time. Asymptotically faster (but more complicated) algorithms are known, but none is so fast as to be in O(n).
Next we ask the question: Is squaring an n-digit number as difficult as multiplying two n-digit numbers? We might hope that something about this special case will allow for a faster algorithm than is required by the more general multiplication problem. However, a simple reduction proof serves to show that squaring is "as hard" as multiplying.
The key to the reduction is the following formula:
The significance of this formula is that it allows us to convert an arbitrary instance of multiplication to a series of operations involving three addition/subtractions (each of which can be done in linear time), two squarings, and a division by 4. Note that the division by 4 can be done in linear time (simply convert to binary, shift right by two digits, and convert back).
This reduction shows that if a linear time algorithm for squaring can be found, it can be used to construct a linear time algorithm for multiplication.
Our next example of reduction concerns the multiplication of two
n×n matrices.
For this problem, we will assume that the values stored in the
matrices are simple integers and that multiplying two simple integers
takes constant time (because multiplication of two int
variables takes a fixed number of machine instructions).
The standard algorithm for multiplying two matrices is to multiply
each element of the first matrix's first row by the corresponding
element of the second matrix's first column, then adding the numbers.
This takes Θ(n) time.
Each of the n2 elements of the solution are computed in
similar fashion, requiring a total of Θ(n3) time.
Faster algorithms are known
(see Strassen's algorithm),
but none are so fast as to be in O(n2).
Now, consider the case of multiplying two symmetric matrices. A symmetric matrix is one in which entry ij is equal to entry ji; that is, the upper-right triangle of the matrix is a mirror image of the lower-left triangle. Is there something about this restricted case that allows us to multiply two symmetric matrices faster than in the general case? The answer is no, as can be seen by the following reduction. Assume that we have been given two n×n matrices A and B. We can construct a 2n×2n symmetric matrix from an arbitrary matrix A as follows:
Here 0 stands for an n×n matrix composed of zero values, A is the original matrix, and AT stands for the transpose of matrix A. [1]
Note that the resulting matrix is now symmetric. We can convert matrix B to a symmetric matrix in a similar manner. If symmetric matrices could be multiplied "quickly" (in particular, if they could be multiplied together in Θ(n2) time), then we could find the result of multiplying two arbitrary n×n matrices in Θ(n2) time by taking advantage of the following observation:
In the above formula, AB is the result of multiplying matrices A and B together.
The following slideshow illustrates this reduction process.
| [1] | The transpose operation takes position ij of the original matrix and places it in position ji of the transpose matrix. This can easily be done in n2 time for an n×n matrix. |