30.20.1.1. Indexing¶

• Goals:

  • Store large files
  • Support multiple search keys
  • Support efficient insert, delete, and range queries

30.20.1.2. Files and Indexing¶

• Entry sequenced file: Order records by time of insertion.

  • Search with sequential search

• Index file: Organized, stores pointers to actual records.

  • Could be organized with a tree or other data structure.

30.20.1.3. Keys and Indexing¶

• Primary Key : A unique identifier for records. May be inconvenient for search.
• Secondary Key: An alternate search key, often not unique for each record. Often used for search key.

30.20.1.4. Linear Indexing (1)¶

• Linear index: Index file organized as a simple sequence of key/record pointer pairs with key values are in sorted order.
• Linear indexing is good for searching variable-length records.

Settings

Saving...
Server Error
Resubmit

30.20.1.5. Linear Indexing (2)¶

• If the index is too large to fit in main memory, a second-level index might be used.

Settings

Saving...
Server Error
Resubmit

30.20.1.6. Tree Indexing (1)¶

• Linear index is poor for insertion/deletion.

• Tree index can efficiently support all desired operations:

  • Insert/delete
  • Multiple search keys (multiple indices)
  • Key range search

30.20.1.7. Tree Indexing (2)¶

Settings

Saving...
Server Error
Resubmit

30.20.1.8. Tree Indexing (3)¶

• Difficulties when storing tree index on disk:

  • Tree must be balanced.
  • Each path from root to leaf should cover few disk pages.

30.20.1.9. Tree Indexing (4)¶

Settings

Saving...
Server Error
Resubmit

30.20.1.10. 2-3 Tree¶

• A 2-3 Tree has the following properties:

  1. A node contains one or two keys
  2. Every internal node has either two children (if it contains one key) or three children (if it contains two keys).
  3. All leaves are at the same level in the tree, so the tree is always height balanced.

• The 2-3 Tree has a search tree property analogous to the BST.

30.20.1.11. 2-3 Tree Example¶

• The advantage of the 2-3 Tree over the BST is that it can be updated at low cost.

30.20.1.12. 2-3 Tree Insertion (1)¶

Settings

Saving...
Server Error
Resubmit

30.20.1.13. 2-3 Tree Insertion (2)¶

Settings

Saving...
Server Error
Resubmit

30.20.1.14. 2-3 Tree Insertion (3)¶

Settings

Saving...
Server Error
Resubmit

30.20.1.15. B-Trees (1)¶

• The B-Tree is an extension of the 2-3 Tree.
• The B-Tree is now the standard file organization for applications requiring insertion, deletion, and key range searches.

30.20.1.16. B-Trees (2)¶

1. B-Trees are always balanced.
2. B-Trees keep similar-valued records together on a disk page, which takes advantage of locality of reference.
3. B-Trees guarantee that every node in the tree will be full at least to a certain minimum percentage. This improves space efficiency while reducing the typical number of disk fetches necessary during a search or update operation.

30.20.1.17. B-Tree Search¶

• Generalizes search in a 2-3 Tree.

  1. Do binary search on keys in current node. If search key is found, then return record. If current node is a leaf node and key is not found, then report an unsuccessful search.
  2. Otherwise, follow the proper branch and repeat the process.

30.20.1.18. B+-Trees¶

• The most commonly implemented form of the B-Tree is the B+-Tree.
• Internal nodes of the B+-Tree do not store record -- only key values to guild the search.
• Leaf nodes store records or pointers to records.
• A leaf node may store more or less records than an internal node stores keys.

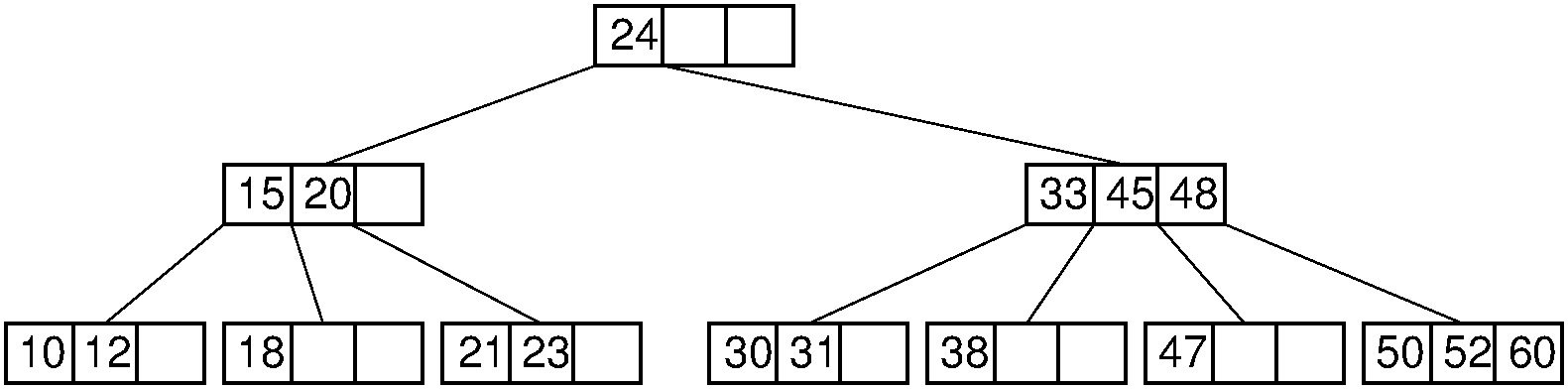
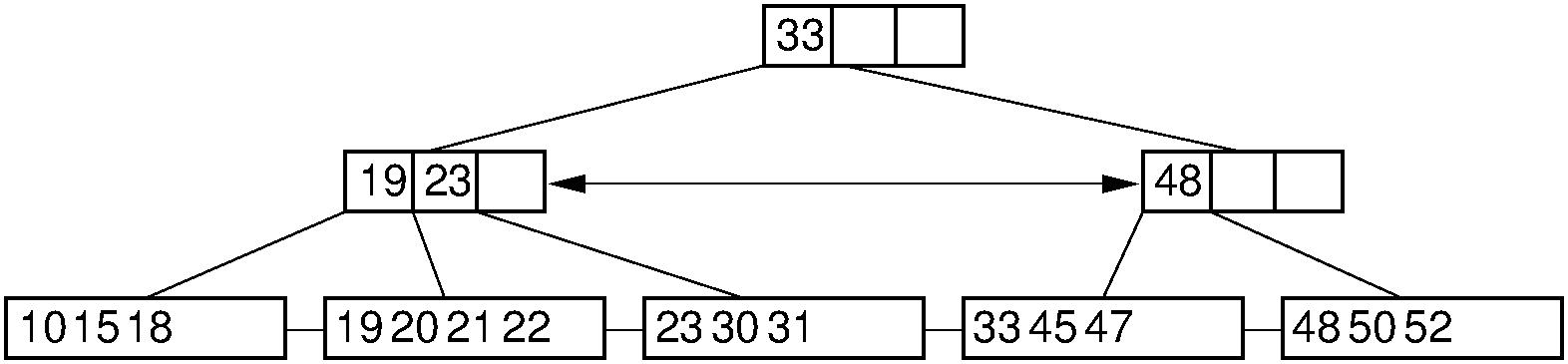
30.20.1.19. B+-Tree Example¶

• In this example, an internal node can have 2 to 4 children
• A leaf node can hold 3 to 5 keys

30.20.1.20. B+-Tree Insertion¶

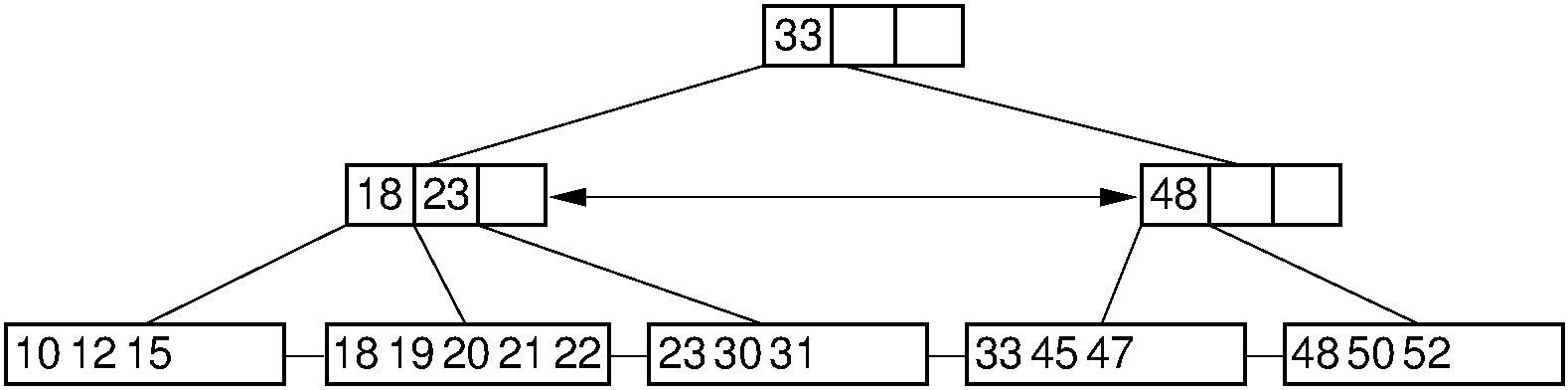
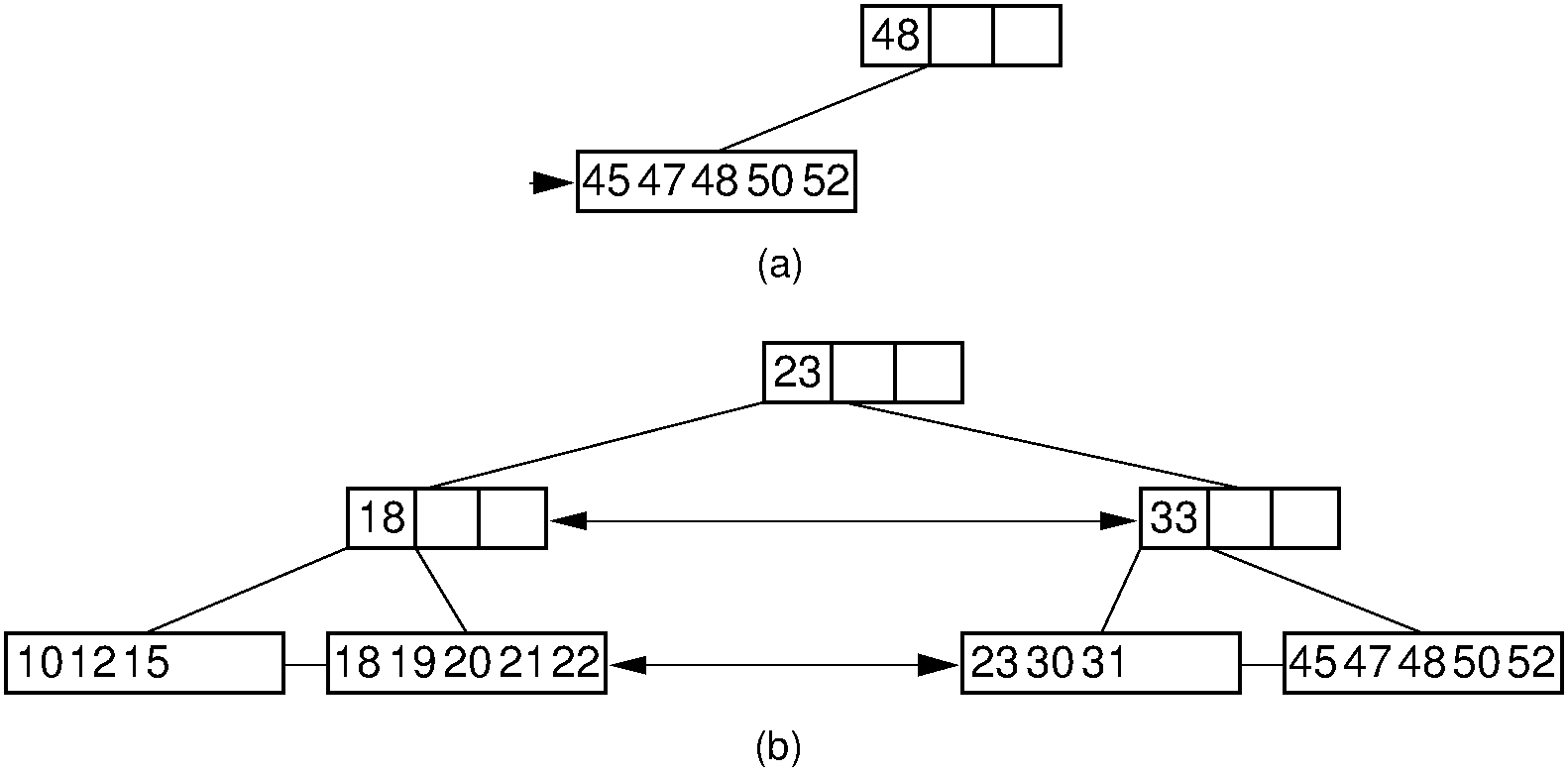
30.20.1.21. B+-Tree Deletion (1)¶

• Delete 18

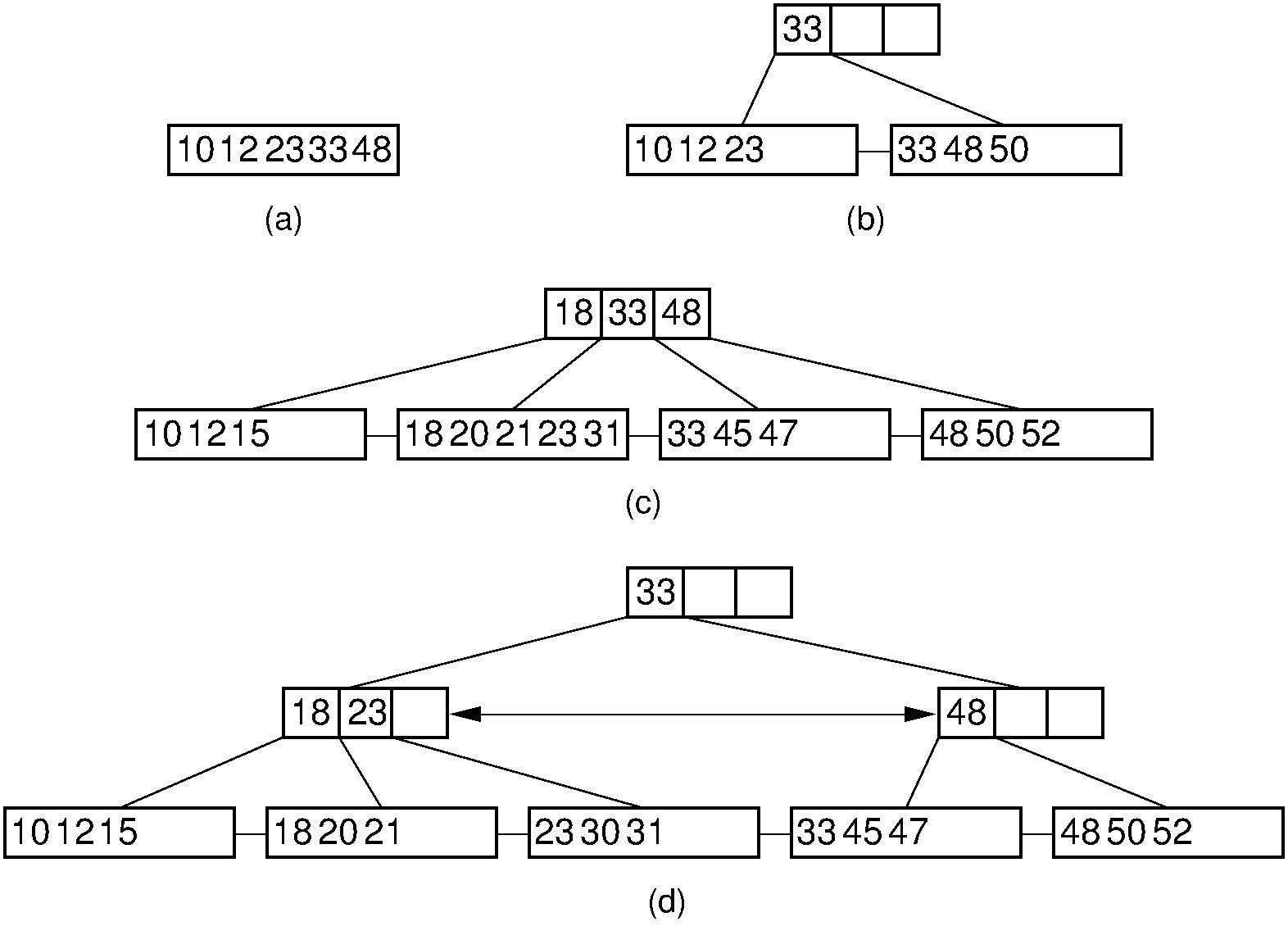
30.20.1.22. B+-Tree Deletion (2)¶

• Delete 12

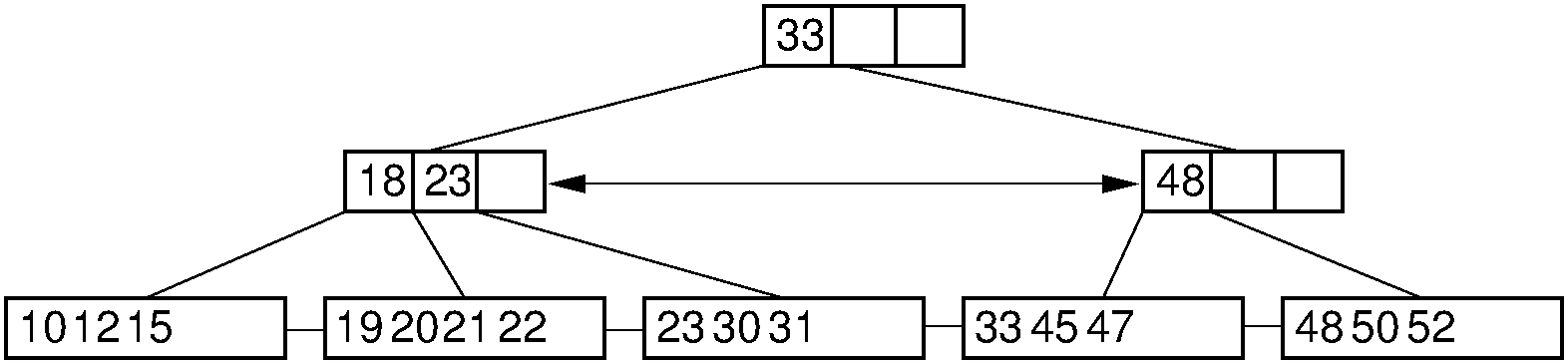
30.20.1.23. B+-Tree Deletion (3)¶

• Delete 33

30.20.1.24. .¶

.

30.20.1.25. B-Tree Space Analysis (1)¶

• B+-Trees nodes are always at least half full.
• The B*-Tree splits two pages for three, and combines three pages into two. In this way, nodes are always 2/3 full.
• Asymptotic cost of search, insertion, and deletion of nodes from B-Trees is \(\Theta(log n)\).
• Base of the log is the (average) branching factor of the tree.

30.20.1.26. B-Tree Space Analysis (2)¶

• Example: Consider a B+-Tree of order 100 with leaf nodes containing 100 records.
• 1 level B+-tree:
• 2 level B+-tree:
• 3 level B+-tree:
• 4 level B+-tree:

• Ways to reduce the number of disk fetches:

  • Keep the upper levels in memory.
  • Manage B+-Tree pages with a buffer pool.

30.20.1.27. B-Trees: The Big Idea¶

• B-trees are really good at managing a sorted list

  • They break the list into manageable chunks
  • The leaves of the B+-tree form the list
  • The internal nodes of the B+-tree merely help find the right chunk