30.21.1.1. Graphs¶

• A graph \(G = (V, E)\) consists of a set of vertices \(V\), and a set of edges \(E\), such that each edge in \(E\) is a connection between a pair of vertices in \(V\).
• The number of vertices is written \(|V|\), and the number edges is written \(|E|\).

30.21.1.2. Paths, Cycles¶

30.21.1.3. Connected Components¶

• The maximum connected subgraphs of an undirected graph are called connected components.

30.21.1.4. Directed Graph Representation¶

30.21.1.5. Undirected Graph Representation¶

30.21.1.6. Representation Space Costs¶

• Adjacency Matrix Space:

  • \(|V|^2\)
  • Small constants

• Adjacency List Space:

  • \(|V| + |E|\)
  • Larger constants

30.21.1.7. Graph ADT¶

interface Graph { // Graph class ADT
  // Initialize the graph with some number of vertices
  void init(int n);

  // Return the number of vertices
  int nodeCount();

  // Return the current number of edges
  int edgeCount();

  // Get the value of node with index v
  Object getValue(int v);

  // Set the value of node with index v
  void setValue(int v, Object val);
  
  // Adds a new edge from node v to node w with weight wgt
  void addEdge(int v, int w, int wgt);

  // Get the weight value for an edge
  int weight(int v, int w);

  // Removes the edge from the graph.
  void removeEdge(int v, int w);

  // Returns true iff the graph has the edge
  boolean hasEdge(int v, int w);

  // Returns an array containing the indicies of the neighbors of v
  int[] neighbors(int v);
}

30.21.1.8. .¶

.

30.21.1.9. Visiting Neighbors¶

  int[] nList = G.neighbors(v);
  for (int i=0; i< nList.length; i++)
    if (G.getValue(nList[i]) != VISITED)
      DoSomething();

30.21.1.10. Graph Traversals¶

• Some applications require visiting every vertex in the graph exactly once.
• The application may require that vertices be visited in some special order based on graph topology.

• Examples:

  • Artificial Intelligence Search
  • Shortest paths problems

30.21.1.11. Graph Traversals (2)¶

• To insure visiting all vertices:

void graphTraverse(Graph G) {
  int v;
  for (v=0; v<G.nodeCount(); v++)
    G.setValue(v, null); // Initialize
  for (v=0; v<G.nodeCount(); v++)
    if (G.getValue(v) != VISITED)
      doTraversal(G, v);
}

30.21.1.12. Depth First Search (1)¶

void DFS(Graph G, int v) {
  PreVisit(G, v);
  G.setValue(v, VISITED);
  int[] nList = G.neighbors(v);
  for (int i=0; i< nList.length; i++)
    if (G.getValue(nList[i]) != VISITED)
      DFS(G, nList[i]);
  PostVisit(G, v);
}

30.21.1.13. Depth First Search (2)¶

Settings

Saving...
Server Error
Resubmit

30.21.1.14. Depth First Search (3)¶

Cost: \(\Theta(|V| + |E|)\).

30.21.1.15. Breadth First Search (1)¶

• Like DFS, but replace stack with a queue.

  • Visit vertex’s neighbors before continuing deeper in the tree.

void BFS(Graph G, int v) {
  LQueue Q = new LQueue(G.nodeCount());
  Q.enqueue(v);
  G.setValue(v, VISITED);
  while (Q.length() > 0) { // Process each vertex on Q
    v = (Integer)Q.dequeue();
    PreVisit(G, v);
    int[] nList = G.neighbors(v);
    for (int i=0; i< nList.length; i++)
      if (G.getValue(nList[i]) != VISITED) { // Put neighbors on Q
        G.setValue(nList[i], VISITED);
        Q.enqueue(nList[i]);
      }
    PostVisit(G, v);
  }
}

30.21.1.16. Breadth First Search (3)¶

Settings

Saving...
Server Error
Resubmit

30.21.1.17. Topological Sort¶

• Problem: Given a set of jobs, courses, etc., with prerequisite constraints, output the jobs in an order that does not violate any of the prerequisites.

30.21.1.18. Depth-First Topological Sort (1)¶

void topsortDFS(Graph G) {
  int v;
  for (v=0; v<G.nodeCount(); v++)
    G.setValue(v, null); // Initialize
  for (v=0; v<G.nodeCount(); v++)
    if (G.getValue(v) != VISITED)
      tophelp(G, v);
}

void tophelp(Graph G, int v) {
  G.setValue(v, VISITED);
  int[] nList = G.neighbors(v);
  for (int i=0; i< nList.length; i++)
    if (G.getValue(nList[i]) != VISITED)
      tophelp(G, nList[i]);
  printout(v);
}

30.21.1.19. Depth-First Topological Sort (1)¶

30.21.1.20. .¶

.

30.21.1.21. Queue-Based Topsort (1)¶

void topsortBFS(Graph G) {          // Topological sort: Queue
  Queue Q = new LQueue(G.nodeCount());
  int[] Count = new int[G.nodeCount()];
  int[] nList;
  int v;
  for (v=0; v<G.nodeCount(); v++) Count[v] = 0; // Initialize
  for (v=0; v<G.nodeCount(); v++) { // Process every edge
    nList = G.neighbors(v);
    for (int i=0; i< nList.length; i++)
      Count[nList[i]]++;            // Add to v's prereq count
  }
  for (v=0; v<G.nodeCount(); v++)   // Initialize Queue
    if (Count[v] == 0)              // V has no prerequisites
      Q.enqueue(v);
  while (Q.length() > 0) {          // Process the vertices
    v = (Integer)Q.dequeue();
    printout(v);                    // PreVisit for Vertex V
    nList = G.neighbors(v);
    for (int i=0; i< nList.length; i++) {
      Count[nList[i]]--;            // One less prerequisite
      if (Count[nList[i]] == 0)     // This vertex is now free
        Q.enqueue(nList[i]);
    }
  }
}

30.21.1.22. .¶

.

30.21.1.23. Queue-Based Topsort (2)¶

30.21.1.24. .¶

.

30.21.1.25. Shortest Paths Problems¶

• Input: A graph with weights or costs associated with each edge.
• Output: The list of edges forming the shortest path.

• Sample problems:

  • Find shortest path between two named vertices
  • Find shortest path from S to all other vertices
  • Find shortest path between all pairs of vertices

• Will actually calculate only distances.

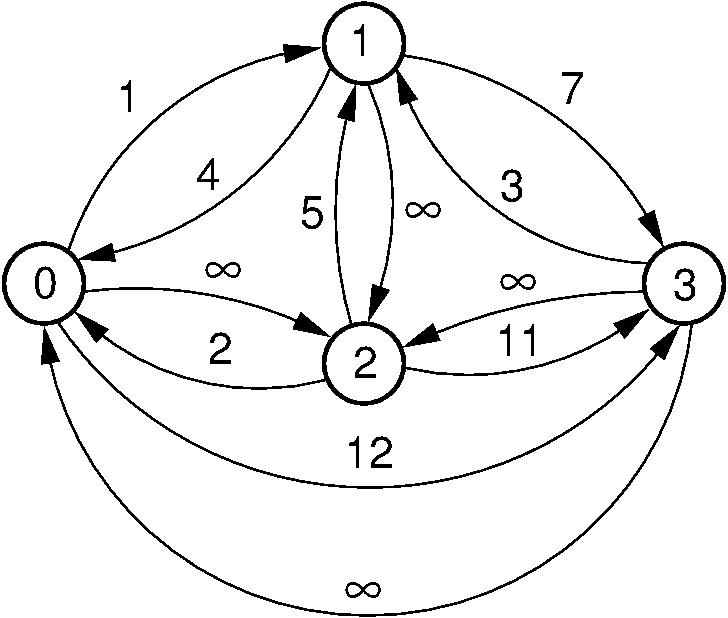
30.21.1.26. Shortest Paths Definitions¶

• \(d(A, B)\) is the shortest distance from vertex \(A\) to \(B\).
• \(w(A, B)\) is the weight of the edge connecting \(A\) to \(B\).
• If there is no such edge, then \(w(A, B) = \infty\).

30.21.1.27. Single-Source Shortest Paths¶

• Given start vertex \(s\), find the shortest path from \(s\) to all other vertices.
• Try 1: Visit vertices in some order, compute shortest paths for all vertices seen so far, then add shortest path to next vertex \(x\).
• Problem: Shortest path to a vertex already processed might go through \(x\).
• Solution: Process vertices in order of distance from \(s\).

30.21.1.28. Dijkstra’s Algorithm Example¶

30.21.1.29. .¶

.

30.21.1.30. Dijkstra’s Implementation¶

// Compute shortest path distances from s, store them in D
void Dijkstra(Graph G, int s, int[] D) {
  for (int i=0; i<G.nodeCount(); i++)    // Initialize
    D[i] = INFINITY;
  D[s] = 0;
  for (int i=0; i<G.nodeCount(); i++) {  // Process the vertices
    int v = minVertex(G, D);     // Find next-closest vertex
    G.setValue(v, VISITED);
    if (D[v] == INFINITY) return; // Unreachable
    int[] nList = G.neighbors(v);
    for (int j=0; j<nList.length; j++) {
      int w = nList[j];
      if (D[w] > (D[v] + G.weight(v, w)))
        D[w] = D[v] + G.weight(v, w);
    }
  }
}

30.21.1.31. Implementing minVertex¶

• Issue: How to determine the next-closest vertex? (I.e., implement minVertex)

• Approach 1: Scan through the table of current distances.

  • Cost: \(\Theta(|V|^2 + |E|) = \Theta(|V|^2)\).

• Approach 2: Store unprocessed vertices using a min-heap to implement a priority queue ordered by \(D\) value. Must update priority queue for each edge.
• Cost: \(\Theta((|V| + |E|)log|V|)\)

30.21.1.32. Approach 1¶

// Find the unvisited vertex with the smalled distance
int minVertex(Graph G, int[] D) {
  int v = 0;  // Initialize v to any unvisited vertex;
  for (int i=0; i<G.nodeCount(); i++)
    if (G.getValue(i) != VISITED) { v = i; break; }
  for (int i=0; i<G.nodeCount(); i++)  // Now find smallest value
    if ((G.getValue(i) != VISITED) && (D[i] < D[v]))
      v = i;
  return v;
}

30.21.1.33. Approach 2¶

// Dijkstra's shortest-paths: priority queue version
void DijkstraPQ(Graph G, int s, int[] D) {
  int v;                                 // The current vertex
  KVPair[] E = new KVPair[G.edgeCount()];        // Heap for edges
  E[0] = new KVPair(0, s);               // Initial vertex
  MinHeap H = new MinHeap(E, 1, G.edgeCount());
  for (int i=0; i<G.nodeCount(); i++)            // Initialize distance
    D[i] = INFINITY;
  D[s] = 0;
  for (int i=0; i<G.nodeCount(); i++) {          // For each vertex
    do { KVPair temp = H.removemin();
         if (temp == null) return;       // Unreachable nodes exist
         v = (Integer)temp.value(); } // Get position
      while (G.getValue(v) == VISITED);
    G.setValue(v, VISITED);
    if (D[v] == INFINITY) return;        // Unreachable
    int[] nList = G.neighbors(v);
    for (int j=0; j<nList.length; j++) {
      int w = nList[j];
      if (D[w] > (D[v] + G.weight(v, w))) { // Update D
        D[w] = D[v] + G.weight(v, w);
        H.insert(D[w], w);
      }
    }
  }
}

30.21.1.34. .¶

.

30.21.1.35. All-pairs Shortest Paths (1)¶

• We could run Shortest Paths starting at each vertex.

• Better is to use Floyd's algorithm.

  • An example of Dynamic Programming
  • Simpler than it sounds: A trivial triple loop

• Define a k-path from vertex \(v\) to vertex \(u\) to be any path whose intermediate vertices (aside from \(v\) and \(u\)) all have indices less than \(k\).

30.21.1.36. All-pairs Shortest Paths (2)¶

30.21.1.37. Floyd's Algorithm¶

/** Compute all-pairs shortest paths */
static void Floyd(Graph G, int[][] D) {
  for (int i=0; i<G.n(); i++) // Initialize D with weights
    for (int j=0; j<G.n(); j++)
      if (G.weight(i, j) != 0) D[i][j] = G.weight(i, j);
  for (int k=0; k<G.n(); k++) // Compute all k paths
    for (int i=0; i<G.n(); i++)
      for (int j=0; j<G.n(); j++)
        if ((D[i][k] != Integer.MAX_VALUE) &&
            (D[k][j] != Integer.MAX_VALUE) &&
            (D[i][j] > (D[i][k] + D[k][j])))
          D[i][j] = D[i][k] + D[k][j];
}

30.21.1.38. Minimal Cost Spanning Trees¶

• Minimal Cost Spanning Tree (MST) Problem:

  • Input: An undirected, connected graph G.

  • Output: The subgraph of G that

    1. has minimum total cost as measured by summing the values of all the edges in the subset, and
    2. keeps the vertices connected.

30.21.1.39. MST Example¶

30.21.1.40. Prim’s MST Algorithm¶

30.21.1.41. .¶

.

30.21.1.42. Implementation 1¶

// Compute shortest distances to the MCST, store them in D.
// V[i] will hold the index for the vertex that is i's parent in the MCST
void Prim(Graph G, int s, int[] D, int[] V) {
  for (int i=0; i<G.nodeCount(); i++)    // Initialize
    D[i] = INFINITY;
  D[s] = 0;
  for (int i=0; i<G.nodeCount(); i++) {  // Process the vertices
    int v = minVertex(G, D);     // Find next-closest vertex
    G.setValue(v, VISITED);
    if (D[v] == INFINITY) return; // Unreachable
    if (v != s) AddEdgetoMST(V[v], v);
    int[] nList = G.neighbors(v);
    for (int j=0; j<nList.length; j++) {
      int w = nList[j];
      if (D[w] > G.weight(v, w)) {
        D[w] = G.weight(v, w);
        V[w] = v;
      }
    }
  }
}

30.21.1.43. Alternate Implementation¶

• As with Dijkstra’s algorithm, the key issue is determining which vertex is next closest.
• As with Dijkstra’s algorithm, the alternative is to use a priority queue.
• Running times for the two implementations are identical to the corresponding Dijkstra’s algorithm implementations.

30.21.1.44. Kruskal’s MST Algorithm (1)¶

• Initially, each vertex is in its own MST.

• Merge two MST’s that have the shortest edge between them.

  • Use a priority queue to order the unprocessed edges. Grab next one at each step.

• How to tell if an edge connects two vertices already in the same MST?

• Use the UNION/FIND algorithm with parent-pointer

  representation.

30.21.1.45. Kruskal’s MST Algorithm (2)¶

30.21.1.46. .¶

.

30.21.1.47. Kruskal’s MST Algorithm (3)¶

• Cost is dominated by the time to remove edges from the heap.

  • Can stop processing edges once all vertices are in the same MST

• Total cost: \(\Theta(|V| + |E| log |E|)\).