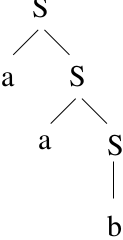
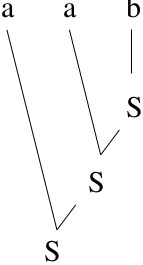
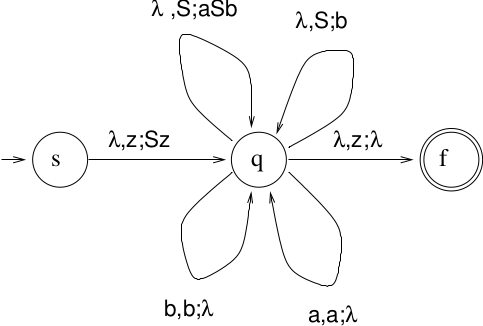
9.1. Parsing¶

9.1.1. Parsing Introduction¶

Parsing: Deciding if $x \in \Sigma^*$ is in $L(G)$ for some CFG $G$ .

Consider the CFG $G$ :

$S \rightarrow Aa$

$A \rightarrow AA \mid ABa \mid \lambda$

$B \rightarrow BBa \mid b \mid \lambda$

Is $ba$ in $L(G)$ ? Running time?

How do you determine whether a string is in $L(G)$ ?

Note: $ba$ is not in $L(G)$ for this $G$ !

Try all possible derivations, but don’t know when to stop. This runs forever!

9.1.2. Introduction Example (2)¶

Same grammar without lambda-rules:

Remove $\lambda$ -rules, then unit productions, and then useless productions from the grammar $G$ above. New grammar $G'$ is:

$S \rightarrow Aa \mid a$

$A \rightarrow AA \mid ABa \mid Aa \mid Ba \mid a$

$B \rightarrow BBa \mid Ba \mid a \mid b$

Is $ba$ in $L(G)$ ? Running time?

Try all possible derivations, there will be at most $|w|$ rounds. NOTE THIS IS NOT LINEAR TIME, IT TAKES A LONG TIME. Actual time is $|w|*p$ where $p$ is the maximum number of rules for any variable.

9.1.3. Introduction Example (3)¶

Grammar:

$S \rightarrow Aa \mid a$

$A \rightarrow AA \mid ABa \mid Aa \mid Ba \mid a$

$B \rightarrow BBa \mid Ba \mid a \mid b$

Consider string $baa$ .

Goal: We would like to only try the rules that give us the derivation and ignore false paths. This would be fast!

$S \Rightarrow Aa \Rightarrow Baa \Rightarrow baa$

9.1.4. Top-down Parser¶

Start with $S$ and try to derive the string.

$S \rightarrow aS \mid b$

Examples: LL Parser, Recursive Descent

9.1.5. Bottom-up Parser¶

Start with string, work backwards, and try to derive $S$ .

Examples: Shift-reduce, Operator-Precedence, LR Parser

9.1.6. Making Parse Tables¶

We want to construct simple tables that tell us:

When you are working on this rule, and see this input, do something

We will use the functions FIRST and FOLLOW to aid in computing parse tables.

Notation that we will use in defining FIRST and FOLLOW.

$G=(V, T, S, P)$

$w, v \in (V \cup T)^*$

$a \in T$

$X, A, B \in V$

$X_I \in (V \cup T)^+$

9.1.7. The function FIRST¶

Definition: $\mbox{FIRST}(w) =$ the set of terminals that begin strings derived from $w$ .

If $w \buildrel * \over \Rightarrow av$ then

$a$ is in $\mbox{FIRST}(w)$

If $w \buildrel * \over \Rightarrow \lambda$ then

$\lambda$ is in $\mbox{FIRST}(w)$

9.1.8. To compute FIRST (1)¶

1. $\mbox{FIRST}(a) = \{a\}$ where a is a terminal.

2. $\mbox{FIRST}(X)$ where $X$ is a variable.

(a) If $X \rightarrow aw$ then

$a$ is in $\mbox{FIRST}(X)$

(b) If $X \rightarrow \lambda$ then

$\lambda$ is in $\mbox{FIRST}(X)$

(c) If $X \rightarrow Aw$ and $\lambda \in \mbox{FIRST}(A)$ then

Everything in $\mbox{FIRST}(w)$ is in $\mbox{FIRST}(X)$

9.1.9. To compute FIRST (2)¶

3. In general, $\mbox{FIRST}(X_1X_2X_3...X_K) =$

* $\mbox{FIRST}(X_1)$

* $\cup\ \mbox{FIRST}(X_2)$ if $\lambda$ is in $\mbox{FIRST}(X_1)$

* $\cup\ \mbox{FIRST}(X_3)$ if $\lambda$ is in $\mbox{FIRST}(X_1)$

and $\lambda$ is in $\mbox{FIRST}(X_2)$

…

* $\cup\ \mbox{FIRST}(X_K)$ if $\lambda$ is in $\mbox{FIRST}(X_1)$

and $\lambda$ is in $\mbox{FIRST}(X_2)$

… and $\lambda$ is in $\mbox{FIRST}(X_{K-1})$

* $-\ \{\lambda\}$ if $\lambda \notin \mbox{FIRST}(X_J)$ for all $J$

(where $X_I$ represents a terminal or a variable)

9.1.10. To compute FIRST (3)¶

We will be computing $\mbox{FIRST}(w)$ where $w$ is the right hand side of a rule.

Thus, we will need to compute $\mbox{FIRST}(X)$ for each symbol $X$ (either terminal or variable) that appears in the right hand side of a rule.

9.1.11. Example (1)¶

$L = \{a^nb^mc^n : n \ge 0, 0 \le m \le 1\}$

$S \rightarrow aSc \mid B$

$B \rightarrow b \mid \lambda$

$\mbox{FIRST}(B) = \{b, \lambda \}$

Using $B \rightarrow b$ gives that $b$ is in $\mbox{FIRST}(B)$ .

Using $B \rightarrow \lambda$ gives that $\lambda$ is in $\mbox{FIRST}(B)$ .

$\mbox{FIRST}(S) = \{a, b, \lambda\}$

Using $S \rightarrow aSc$ gives that $a$ is in $\mbox{FIRST}(S)$ .

Using $S \rightarrow B$ and $\lambda$ is in $\mbox{FIRST}(B)$ gives that everything in $\mbox{FIRST}(B)$ is in $\mbox{FIRST}(S)$ , so $b$ and $\lambda$ are in $\mbox{FIRST}(S)$ .

$\mbox{FIRST}(Sc) = \{a, b, c\}$

9.1.12. Example (2a)¶

$S \rightarrow BCD \mid aD$

$A \rightarrow CEB \mid aA$

$B \rightarrow b \mid \lambda$

$C \rightarrow dB \mid \lambda$

$D \rightarrow cA \mid \lambda$

$E \rightarrow e \mid fE$

9.1.13. Example (2b)¶

$\mbox{FIRST}(B) =$

$\mbox{FIRST}(C) =$

$\mbox{FIRST}(D) =$

$\mbox{FIRST}(E) =$

$\mbox{FIRST}(A) =$

$\mbox{FIRST}(S) =$

9.1.14. The function FOLLOW¶

Definition: $\mbox{FOLLOW}(X) =$ set of terminals that can appear to the right of $X$ in some derivation.

(We only compute FOLLOW for variables.)

If $S \buildrel * \over \Rightarrow wAav$ then

$a$ is in $\mbox{FOLLOW}(A)$

(where $w$ and $v$ are strings of terminals and variables, $a$ is a terminal, and $A$ is a variable)

9.1.15. Computing FOLLOW¶

$\$$ is in $\mbox{FOLLOW}(S)$

If $A \rightarrow wBv$ and $v \ne \lambda$ then

$\mbox{FIRST}(v) - \{ \lambda \}$ is in $\mbox{FOLLOW}(B)$

If $A \rightarrow wB$ or $A \rightarrow wBv$ and $\lambda$ is in $\mbox{FIRST}(v)$ then

$\mbox{FOLLOW}(A)$ is in $\mbox{FOLLOW}(B)$

$\lambda$ is never in FOLLOW

9.1.16. Example (1)¶

$S \rightarrow aSc \mid B$

$B \rightarrow b \mid \lambda$

Reminder: $\lambda$ is never in a FOLLOW set.

$\mbox{FOLLOW}(S) = \{ \$, c \}$

$\$$ goes into $\mbox{FOLLOW}(S)$ by rule 1. Then $c$ goes into $\mbox{FOLLOW}(S)$ by rule 2 since $S \rightarrow aSc$ and $\mbox{FIRST}(c) = \{c\}$ .

$\mbox{FOLLOW}(B) = \{ \$, c \}$

By rule 3 and $S \rightarrow B$ , $\mbox{FOLLOW}(S)$ is added to $\mbox{FOLLOW}(B)$ .

9.1.17. Example (2a)¶

$S \rightarrow BCD \mid aD$

$A \rightarrow CEB \mid aA$

$B \rightarrow b \mid \lambda$

$C \rightarrow dB \mid \lambda$

$D \rightarrow cA \mid \lambda$

$E \rightarrow e \mid fE$

9.1.18. Example (2b)¶

$\mbox{FOLLOW}(S) =$

$\mbox{FOLLOW}(A) =$

$\mbox{FOLLOW}(B) =$

$\mbox{FOLLOW}(C) =$

$\mbox{FOLLOW}(D) =$

$\mbox{FOLLOW}(E) =$

9.1.19. LL(k) Parsing¶

We discussed this in principle before. Now we want to operationalize it.

Note: A language is not LL(k), a grammar is.

$L = \{a^iabc^i \mid i > 0 \}$

$G_1 = S \rightarrow aSc \qquad \{aaa\}$

$S \rightarrow aabc \qquad \{aab\}$

$G_2 = S \rightarrow aA$

$A \rightarrow Sc \qquad \{aa\}$

$A \rightarrow abc \qquad \{ab\}$

$G_3 = S \rightarrow aaAc$

$A \rightarrow aAc \quad \{a\}$

$A \rightarrow b \qquad \{b\}$

9.1.20. LL parsing process¶

First, convert CFG to PDA

$L = \{a^nbb^n: n \ge 0 \}$

$S \rightarrow aSb \mid b$

The PDA is nondeterministic.

Use lookahead to make it deterministic: determine which rewrite rule to use.

9.1.21. Parsing routine (for this grammar)¶

symbol is the lookahead symbol and $ is the end-of-string marker:

state = s
push(S)
state = q
read(symbol)                               obtain the lookahead symbol
while top-of-stack <> z do                 while stack is not empty
   case top-of-stack of
   S: if symbol == a then                  cases for variables
            { pop(); push(aSb) }           replace S by aSb
         else if symbol == b then
            { pop(); push(b) }             replace S by b
         else error
      a: if symbol <> a, then error        cases for terminals
         else { pop(); read(symbol) }      pop a, get next lookahead
      b: if symbol <> b, then error
         else { pop(); read(symbol) }      pop b, get next lookahead
      end case
end while
pop()                                      pop z from the stack
if symbol <> $ then error
state = f

9.1.22. LL Parse Table¶

When the grammar is large, the parsing routine will have many cases.

Alternatively, store the information for which rule to apply in a table.

Rows: variables

Columns: terminals, $ (end of string marker)

LL[i,j] contains the right-hand-side of a rule. This right-hand-side is pushed onto the stack when the left-hand-side of the rule is the variable representing the $i$ th row and the lookahead is the symbol representing the $j$ th column.

For any CFG that we can specify by this type of parse table, we can use a generic parser to determine if strings are in this language.

Gets rid of use of states

9.1.23. Parse Table Example¶

Parse table for

$L = \{a^nbb^n: n \ge 0 \}$

$S \rightarrow aSb \mid b$

$\begin{split}\begin{array}{c||c|c|c} & a & b & \$ \\ \hline \hline S & aSb & b & \mbox{error} \\ \end{array}\end{split}$

Example strings:

aabbb

b

9.1.24. A generic parsing routine¶

(LL[,] is the parse table.):

push(S)
read(symbol)                                         obtain the lookahead symbol
while stack not empty do
   case top-of-stack of
      terminal:
         if top-of-stack == symbol
            then { pop(); read(symbol) }             pop terminal and get next lookahead
         else
            error
      variable:
         if LL[top-of-stack, symbol] <> error
            then { pop(),                            pop the lhs
                   push(LL[top-of-stack,symbol]) }   push the rhs
            else
               error
      end case
end while
if symbol <> $, then error

9.1.25. Example¶

$S \rightarrow aSb$

$S \rightarrow c$

$\begin{split}\begin{array}{l||l|l|l|l} &a&b&c&\$ \\ \hline \hline S & aSb & \mbox{error} & c & \mbox{error} \\ \end{array}\end{split}$

When $S$ is on the stack and $a$ is the lookahead, replace $S$ by $aSb$

When $S$ is on the stack and $b$ is the lookahead, there is an error (there must be a $c$ between the $a$ ‘s and $b$ ‘s)

When $S$ is on the stack and $ is the lookahead, then there is an error ( $S$ must be replaced by at least one terminal)

When $S$ is on the stack, and $c$ is the lookahead, then $S$ should be replaced by $c$ .

9.1.26. Example¶

$S \rightarrow Ac \mid Bc$

$A \rightarrow aAb \mid \lambda$

$B \rightarrow b$

When the grammar has a $\lambda$ -rule, it can be difficult to compute parse tables.

In this example, $A$ can disappear (due to $A \rightarrow \lambda$ ).

So when $S$ is on the stack, it can be replaced by $Ac$ if either “a” or “c” are the lookahead, or it can be replaced by $Bc$ if “b” is the lookahead.

9.1.27. Constructing an LL parse table¶

1. For each rule $A \rightarrow w$

a. For each a in FIRST(w)

add w to LL[A,a]

b. If $\lambda$ is in FIRST(w)

add $w$ to LL[A,b] for each $b$ in FOLLOW(A)

where $b \in T \cup \{\$\}$

2. Each undefined entry is an error.

9.1.28. Example (1): Need FIRST and FOLLOW¶

$S \rightarrow aSc \mid B$

$B \rightarrow b \mid \lambda$

We have already calculated FIRST and FOLLOW for this Grammar:

$\begin{split}\begin{array}{c|l|l} & FIRST & FOLLOW\\ \hline \hline S & a, b, \lambda & \$, c \\ B & b, \lambda & \$, c \\ \end{array}\end{split}$

9.1.29. Example (2): Compute Parse Table¶

For $S \rightarrow aSc$ , $\mbox{FIRST}(aSc) = \{a\}$ , so add $aSc$ to LL[S,a] by step 1a.

For $S \rightarrow B$ ,

$\mbox{FIRST}(B) = \{b, \lambda \}$

$\mbox{FOLLOW}(S) = \{\$, c\}$

By step 1a, add $B$ to LL[S,b]

By step 1b, add $B$ to LL[S,c] and LL[S,$]

For $B \rightarrow b$ , $\mbox{FIRST}(b) = \{b\}$ , so by step 1a add $b$ to LL[B,b]

For $B \rightarrow \lambda$ $\mbox{FIRST}(\lambda) = \{ \lambda \}$ and $\mbox{FOLLOW}(B) = \{\$, c\}$ ,

so by step 1b add $\lambda$ to LL[B,c] and add $\lambda$ to LL[B,$].

9.1.30. Example (3): Sample Trace¶

$\begin{split}\begin{array}{c||c|c|c|c} & a & b & c & \$ \\ \hline \hline S & aSc & B & B & B \\ \hline B & \mbox{error} & b & \lambda & \lambda \end{array}\end{split}$

Parse string: $aacc$

$\begin{split}\begin{array}{lcccccccc} &&&&a \\ &&a&&S &S &B \\ &&S& S& c& c& c& c \\ \mbox{Stack:} & \underline{S} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} \\ \mbox{symbol:} & a & a & a' & a' & c & c& c& c' \\ \end{array}\end{split}$

where $a'$ is the second $a$ in the string and symbol is the lookahead symbol. This table is an LL(1) table because only 1 symbol of lookahead is needed.

9.1.31. Example (4): Sample Trace¶

Trace $aabcc$

$\begin{split}\begin{array}{lccccccccc} &&&&a \\ &&a&&S &S &B & b\\ &&S& S& c& c& c& c & c \\ \mbox{Stack:} & \underline{S} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} & \underline{c} \\ \mbox{symbol:} & a & a & a' & a' & b & b& b& c & c' \\ \end{array}\end{split}$

where $a'$ is the second $a$ in the string and symbol is the lookahead symbol. This table is an LL(1) table because only 1 symbol of lookahead is needed.

9.1.32. LL(k) Can’t Parse All CFGs¶

$L = \{a^n: n \ge 0 \} \cup \{a^nb^n: n \ge 0 \}$

$S \rightarrow A$

$S \rightarrow B$

$A \rightarrow aA$

$A \rightarrow \lambda$

$B \rightarrow aBb$

$B \rightarrow \lambda$

This grammar cannot be recognized by an LL(k) parser for any $k$ .

Consider the string $aabb$ . Need 3 lookahead to realize that we want $S \rightarrow B$ .

For $aaabbb$ , we need 4 lookahead.

For $a^nb^n$ , we need $n$ lookahead.

9.1.33. Conclusion¶

There are some CFL’s that have no LL(k) Parser

There are some languages for which some grammars have LL(k) parsers and some don’t.

Partial Coursenotes for Formal Languages and Automata

Chapter 9 Extra

9.1. Parsing¶

9.1.1. Parsing Introduction¶

9.1.2. Introduction Example (2)¶

9.1.3. Introduction Example (3)¶

9.1.4. Top-down Parser¶

9.1.5. Bottom-up Parser¶

9.1.6. Making Parse Tables¶

9.1.7. The function FIRST¶

9.1.8. To compute FIRST (1)¶

9.1.9. To compute FIRST (2)¶

9.1.10. To compute FIRST (3)¶

9.1.11. Example (1)¶

9.1.12. Example (2a)¶

9.1.13. Example (2b)¶

9.1.14. The function FOLLOW¶

9.1.15. Computing FOLLOW¶

9.1.16. Example (1)¶

9.1.17. Example (2a)¶

9.1.18. Example (2b)¶

9.1.19. LL(k) Parsing¶

9.1.20. LL parsing process¶

9.1.21. Parsing routine (for this grammar)¶

9.1.22. LL Parse Table¶

9.1.23. Parse Table Example¶

9.1.24. A generic parsing routine¶

9.1.25. Example¶

9.1.26. Example¶

9.1.27. Constructing an LL parse table¶

9.1.28. Example (1): Need FIRST and FOLLOW¶

9.1.29. Example (2): Compute Parse Table¶

9.1.30. Example (3): Sample Trace¶

9.1.31. Example (4): Sample Trace¶

9.1.32. LL(k) Can’t Parse All CFGs¶

9.1.33. Conclusion¶