9.2. Properties Stuff¶
9.2.1. Properties and Proving: Problem 1(a)¶
Consider the property Replace_one_a_with_b or R1awb for short. If \(L\) is regular, prove that R1awb(\(L\)) is regular.
The property R1awb applied to a language \(L\) replaces one \(a\) in each string with a \(b\). If a string does not have an \(a\), then the string is not in R1awb(\(L\)).
What does this mean? What are we trying to prove?
Example 1: Consider \(L = \{aaab, bbaa\}\)
IS \(L\) REGULAR? YES, you can apply the property.
\(\mathrm{R1awb}(L) = \{baab, abab, aabb, bbba, bbab\}\)
9.2.2. Properties and Proving: Problem 1(b)¶
Example 2: Consider \(\Sigma=\{a, b\}\), \(L = \{w \in \Sigma^{*} \mid w \mathrm{\ has\ an\ even\ number\ of\ } a's \mathrm{\ and\ an\ even\ number\ of\ } b's \}\)
Is \(L\) regular? YES, How do you know? We built a DFA for this language.
\(\mathrm{R1awb}(L) = \{w \in \Sigma^{*} \mid w \mathrm{\ has\ an\ odd\ number\ of\ } a's \mathrm{\ and\ an\ odd\ number\ of\ } b's\}\)
9.2.3. Proof¶
9.2.4. Properties and Proving: Problem 2¶
Consider the property Truncate_all_preceeding_b’s or TruncPreb for short. If \(L\) is regular, prove TruncPreb(\(L\)) is regular.
The property TruncPreb applied to a language \(L\) removes all preceeding b’s in each string. If a string does not have an preceeding b, then the string is the same in TruncPreb(\(L\)).
What does this mean? What are we trying to prove?
9.2.5. Examples¶
Example 1: Consider \(L = \{aaab, bbaa\}\)
IS \(L\) REGULAR? YES, you can apply the property.
\(\mathrm{TruncPreb}(L) = \{aaab, aa\}\)
Example 2: Consider \(L = \{(bba)^n \mid n > 0\}\)
Is \(L\) regular? YES. How do you know? We built a DFA for this language.
<< List out possible strings in the language >>
9.2.6. Theorem and Proof (1)¶
9.2.7. Theorem and Proof (2)¶
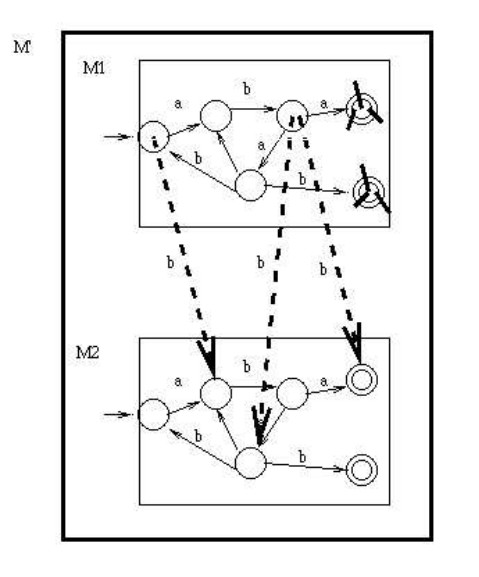
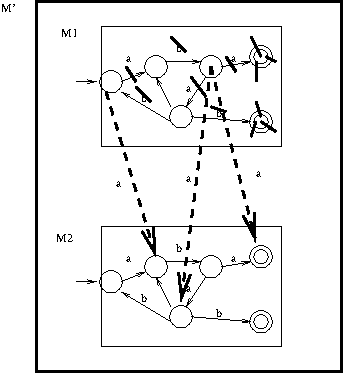
Make a copy of the DFA. For each a arc in the first copy, remove it and instead have the \(a\) arc go to the corresponding destination below.
For each \(b\) arc in the first copy, change the \(b\) to lambda.