Major Concepts¶
1. Introduction¶
In this module, we present basic notation needed to discuss the three major concepts for the semester:
- Languages
- Grammars
- Automata
2. Languages¶
- \(\Sigma\): A set of symbols, an alphabet
- string: Finite sequence of symbols (from some alphabet)
- language: A set of strings defined over \(\Sigma\)
Languages are sets, a subset of the powerset of \(\Sigma\)
2.1. Examples¶
\(\Sigma = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\)
\(L = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ... \}\)
\(\Sigma = \{a, b, c\}\)
\(L = \{ab, ac, cabb\}\)
\(L\) is a language with 3 strings, each string is a sequence of strings formed over the alphabet.
How any strings could be in \(L\)?
\(\Sigma = \{a, b\}\)
\(L = \{a^n b^n | n > 0\}\)
This is an example of an infinite language.
What are the strings in the language? \(\{ab, aabb, aaabbb, aaaabbbb, . . .\}\)
2.2. Notation¶
- Symbols in alphabet: \(a, b, c, d, ...\)
- String names: \(u,v,w,...\)
2.3. Definition of concatenation¶
Let \(w = a_1a_2...a_n\) and \(v=b_1b_2...b_n\)
Then, \(w \circ v\) OR \(wv=a_1a_2...a_nb_1b_2...b_m\).
2.4. String Operations¶
Strings: \(w=abbc\), \(v=ab\), \(u=c\)
Size of string
\(|w| + |v| = 6\)
Concatenation
\(v^3 = vvv = v \circ v \circ v = ababab\)
\(v^0 = \lambda\)
\(w^R = cbba\)
\(|vv^Rw|= 8\)
\(ab \circ λ = ab\)
\(\Sigma^∗ =\) set of strings obtained by concatenating 0 or more symbols from \(\Sigma\)
Examples:
\(\Sigma = \{a, b\}\)
\(\Sigma^* = \{\lambda, a, b, aa, ab, ba, bb, ...\}\)
Note: Easiest to list out all the strings of length 0, then length 1, then length 2, etc.
\(\Sigma^+ = \Sigma^* - \{\lambda\}\)
More Examples:
\(\Sigma = \{a, b, c\}, L_1=\{ab, bc, aba\}, L_2 = \{c, bc, bcc\}\)
- \(L_1 \cup L_2 = \{ab, bc, aba, c, bcc\}\)
- \(L_1 \cap L_2 = \{bc\}\)
- \(\overline{L_1} = \Sigma{}^{*} - L\)
- \(\overline{L_1 \cap L_2} = \Sigma{}^{*} - \{bc\}\)
- \(L_1 \circ L_2 = \{xy \mid x \in L_1\) and \(y\in L_2\} = \{abc, abbc, abbcc, bcc, bcbc, bcbcc, abac, ababc, ababcc\}\)
2.5. Definitions¶
\(L^0 = \{\lambda\}\)
\(L^2 = L \circ L\)
\(L^3 = L \circ L \circ L\)
\(L^{*} = L^0 \cup L^1 \cup L^2 \cup L^3 \ldots\)
\(L^{+} = L^1 \cup L^2 \cup L^3 \ldots\)
3. Grammars¶
Before looking at formal grammars to define formal languages and programming languages, let's look at a grammar you can maybe relate to, a grammar for english. This will be a tiny subset of the english language, not complete by far!
<sentence> \(\rightarrow\) <subject><verb><d.o.>
<subject> \(\rightarrow\) <noun> | <article><noun>
<verb> \(\rightarrow\) hit | ran | ate
<d.o.> \(\rightarrow\) <article><noun> | <noun>
<noun> \(\rightarrow\) Fritz | ball
<article> \(\rightarrow\) the | an | a
Note that any grammar has variables (non-terminals) and terminals. Terminals are generally strings. Variables are things that ultimately are replaced by terminals. In this example, we put \(<>\) brackets around all of the variables to make them easier to recognize. We won't always do this. The grammar has a collection of productions. In this example, each production replaces a variable with some series of variables and terminals. Ultimately, all "sentences" in the "language" are generated by starting with the <sentence> variable, and using productions to reach the desired sentence.
3.1. Examples¶
Deriving a sentence: To derive a sentence, start at the starting point of the grammar and do replacements until you can do no more replacements. A variable in the grammar can be replaced by the right hand side of its rule:
Fritz hit the ball
<sentence> -> <subject><verb><d.o>
-> <noun><verb><d.o>
-> Fritz <verb><d.o.>
-> Fritz hit <d.o.>
-> Fritz hit <article><noun>
-> Fritz hit the <noun>
-> Fritz hit the ball
Can we derive these sentences? If not, can we change the grammar?:
The ball hit Fritz
The ball ate the ball
- A sentence is syntactically correct if it follows the rules (the grammar can dervive it)
- A sentence is semantically correct if it has "meaning"
3.2. Formal definition of a grammar¶
A grammar \(G = (V, T, S, P)\) where
\(V\) is a finite set of variables (nonterminals).
\(T\) is a finite set of terminals (generally, these are strings).
\(S\) is the start variable (\(S \in V\)).
\(P\) is a set of productions (rules).
\(x \rightarrow y\) means to replace \(x\) by \(y\).
Here, \(x \in (V \cup T)^+, y \in (V \cup T)^*\).
Todo
| type: | Question |
|---|
Is this really correct? In this example, x is a single non-terminal. In general, we can't have just a terminal on the left side, can we? Later, more complicated grammars might have a series of things on the left side with suitable restrictions. Do we want to bring that up here?
Question: What are \(S, T, V, P\) in the "english" grammar example above?
3.3. Notation¶
Given grammar \(G = (V, T, S, P)\), define
Now, try to describe in words: What is the language of the grammar? Answer: It is all strings formed over the alphabet (or set of terminals, note that \(T^*\) is all possible strings over T), SUCH THAT if you start with S (the start symbol in the grammar), you can derive the string.
Example
\(G=(\{S\}, \{a,b\}, S, P)\)
\(P=\{S \rightarrow aaS, S \rightarrow b\}\)
\(L(G) =\) ?
Answer: \(\{b, aab, aaaab, ... \} = \{(aa)^nb | n \ge 0\}\)
Example
\(L(G) = \{a^nccb^n | n > 0\}\)
\(G =\) ?
Answer:
\(S \rightarrow aSb | aAb\)
\(A \rightarrow cc\)
Example
\(G = (\{S\}, \{a,b\}, S, P)\)
\(P = \{S \rightarrow aSb, S \rightarrow SS, S \rightarrow ab\}\)
Which of these strings \(aabb, abab, abba, babab\) can be generated by this grammar? Show the derivations.
\(L(G) =\) ?
Answer:
The language of matching parenthesis where \(a\) is left paren, and \(b\) is right paren.
\(S \rightarrow aSb \rightarrow aabb\)
\(S \rightarrow SS \rightarrow abS \rightarrow abab\)
Cannot derive \(abba, babab\). WHY? Nothing ends with \(a\), nothing starts with \(b\).
4. Automata¶
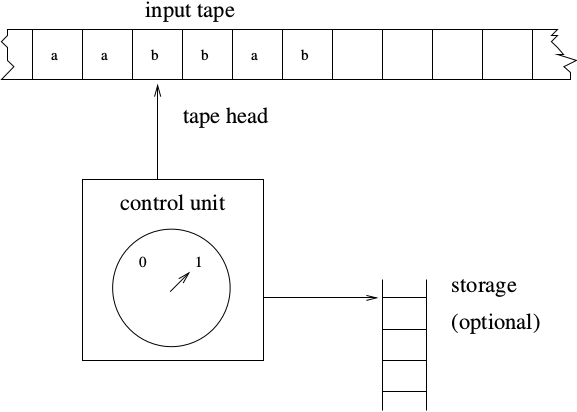
Figure 1: Abstract model of a digital computer. Note that in the control unit, the numbers are symbolizing "states", which are the specific positions on the dial that the arrow may point to. While this picture shows the physical components of the "computer", it is not showing the control behavior (what to do if in a given state with a given symbol on the current square of the tape, and a given value at the current position in the storage unit). This control behavior is like the "software" of the computer.
There is a program associated with the control unit, and the input is processed once from left to right. Some versions have an additional storage unit. We will define specific automata throughout the semester.
This is the topic for the next chapter.


