31.2. Lower Bounds on Searching Lists¶
The sorting lower bound proof is important because it shows that the problem of sorting is \(\Theta(n \log n)\) in the worst case. There are a number of algorithms to search in sorted and unsorted lists, and it would be nice to know the lower bound to this important problem. We will extend our pool of techniques for lower bounds proofs in this section by studying lower bounds for searching unsorted and sorted lists.
31.2.1. Searching in Unsorted Lists¶
Given an (unsorted) list L of \(n\) elements and a search key \(K\), we seek to identify one element in L which has key value \(k\), if any exists. For the rest of this discussion, we will assume that the key values for the elements in L are unique, that the set of all possible keys is totally ordered (that is, the operations \(<\), \(=\), and \(>\) are defined for all pairs of key values), and that comparison is our only way to find the relative ordering of two keys. Our goal is to solve the problem using the minimum number of comparisons.
Given this definition for searching, we can easily come up with the standard sequential search algorithm, and we can also see that the lower bound for this problem is "obviously" \(n\) comparisons. (Keep in mind that the key \(K\) might not actually appear in the list.) However, lower bounds proofs are a bit slippery, and it is instructive to see how they can go wrong.
Theorem 31.2.1
The lower bound for the problem of searching in an unsorted list is \(n\) comparisons.
Here is our first attempt at proving the theorem.
Proof 1
We will try a proof by contradiction. Assume an algorithm \(A\) exists that requires only \(n-1\) (or less) comparisons of \(K\) with elements of L. Because there are \(n\) elements of L, \(A\) must have avoided comparing \(K\) with L [\(i\)] for some value \(i\). We can feed the algorithm an input with \(K\) in position \(i\). Such an input is legal in our model, so the algorithm is incorrect.
Is this proof correct? Unfortunately no. First of all, any given algorithm need not necessarily consistently skip any given position \(i\) in its \(n-1\) searches. For example, it is not necessary that all algorithms search the list from left to right. It is not even necessary that all algorithms search the same \(n-1\) positions first each time through the list. Perhaps it picks them at random.
We can try to dress up the proof as follows.
Proof 2
On any given run of the algorithm, if \(n-1\) elements are compared against \(K\), then some element position (call it position \(i\)) gets skipped. It is possible that \(K\) is in position \(i\) at that time, and will not be found. Therefore, \(n\) comparisons are required.
Unfortunately, there is another error that needs to be fixed. It is not true that all algorithms for solving the problem must work by comparing elements of L against \(K\). An algorithm might make useful progress by comparing elements of L against each other. For example, if we compare two elements of L, then compare the greater against \(K\) and find that this element is less than \(K\), we know that the other element is also less than \(K\). It seems intuitively obvious that such comparisons won't actually lead to a faster algorithm, but how do we know for sure? We somehow need to generalize the proof to account for this approach.
We will now present a useful abstraction for expressing the state of knowledge for the value relationships among a set of objects. A total order defines relationships within a collection of objects such that for every pair of objects, one is greater than the other. A partially ordered set or poset is a set on which only a partial order is defined. That is, there can be pairs of elements for which we cannot decide which is "greater". For our purpose here, the partial order is the state of our current knowledge about the objects, such that zero or more of the order relations between pairs of elements are known. We can represent this knowledge by drawing directed acyclic graphs (DAGs) showing the known relationships, as illustrated by Figure 31.2.1.
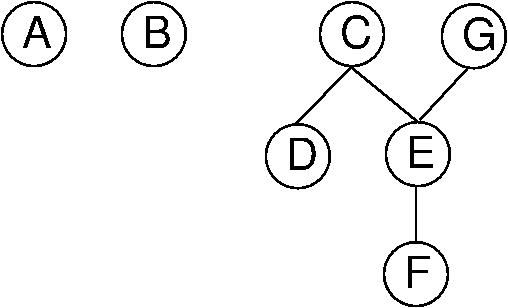
Figure 31.2.1: Illustration of using a poset to model our current knowledge of the relationships among a collection of objects. A directed acyclic graph (DAG) is used to draw the poset (assume all edges are directed downward). In this example, our knowledge is such that we don't know how \(A\) or \(B\) relate to any of the other objects. However, we know that both \(C\) and \(G\) are greater than \(E\) and \(F\). Further, we know that \(C\) is greater than \(D\), and that \(E\) is greater than \(F\)
Proof 3
Initially, we know nothing about the relative order of the elements in L, or their relationship to \(K\). So initially, we can view the \(n\) elements in L as being in \(n\) separate partial orders. Any comparison between two elements in L can affect the structure of the partial orders.
Now, every comparison between elements in L can at best combine two of the partial orders together. Any comparison between \(K\) and an element, say \(A\), in L can at best eliminate the partial order that contains \(A\). Thus, if we spend \(m\) comparisons comparing elements in L we have at least \(n-m\) partial orders. Every such partial order needs at least one comparison against \(K\) to make sure that \(K\) is not somewhere in that partial order. Thus, any algorithm must make at least \(n\) comparisons in the worst case.
31.2.2. Searching in Sorted Lists¶
We will now assume that list L is sorted. In this case, is linear search still optimal? Clearly no, but why not? Because we have additional information to work with that we do not have when the list is unsorted. We know that the standard binary search algorithm has a worst case cost of \(O(\log n)\). Can we do better than this? We can prove that this is the best possible in the worst case with a proof similar to that used to show the lower bound on sorting.
Again we use the decision tree to model our algorithm. Unlike when searching an unsorted list, comparisons between elements of L tell us nothing new about their relative order, so we consider only comparisons between \(K\) and an element in L. At the root of the decision tree, our knowledge rules out no positions in L, so all are potential candidates. As we take branches in the decision tree based on the result of comparing \(K\) to an element in L, we gradually rule out potential candidates. Eventually we reach a leaf node in the tree representing the single position in L that can contain \(K\). There must be at least \(n+1\) nodes in the tree because we have \(n+1\) distinct positions that \(K\) can be in (any position in L, plus not in L at all). Some path in the tree must be at least \(\log n\) levels deep, and the deepest node in the tree represents the worst case for that algorithm. Thus, any algorithm on a sorted array requires at least \(\Omega(\log n)\) comparisons in the worst case.
We can modify this proof to find the average cost lower bound. Again, we model algorithms using decision trees. Except now we are interested not in the depth of the deepest node (the worst case) and therefore the tree with the least-deepest node. Instead, we are interested in knowing what the minimum possible is for the "average depth" of the leaf nodes. Define the total path length as the sum of the levels for each node. The cost of an outcome is the level of the corresponding node plus 1. The average cost of the algorithm is the average cost of the outcomes (total path length / \(n\)). What is the tree with the least average depth? This is equivalent to the tree that corresponds to binary search. Thus, binary search is optimal in the average case.
While binary search is indeed an optimal algorithm for a sorted list in the worst and average cases when searching a sorted array, there are a number of circumstances that might lead us to select another algorithm instead. One possibility is that we know something about the distribution of the data in the array. If each position in L is equally likely to hold \(K\) (equivalently, the data are well distributed along the full key range), then an interpolation search is \(\Theta(\log \log n)\) in the average case. If the data are not sorted, then using binary search requires us to pay the cost of sorting the list in advance, which is only worthwhile if many (at least \(O(\log n)\) searches will be performed on the list. Binary search also requires that the list (even if sorted) be implemented using an array or some other structure that supports random access to all elements with equal cost. Finally, if we know all search requests in advance, we might prefer to sort the list by frequency and do linear search in extreme search distributions, or use a self-organizing list.


