17.10. Hashing¶
17.10.1. Hashing¶
17.10.1.1. Hashing (1)¶
Hashing: The process of mapping a key value to a position in a table.
A hash function maps key values to positions. It is denoted by \(h\).
A hash table is an array that holds the records. It is denoted by HT.
HT has \(M\) slots, indexed form 0 to \(M-1\).
17.10.1.2. Hashing (2)¶
For any value \(K\) in the key range and some hash function \(h\), \(h(K) = i\), \(0 <= i < M\), such that key(HT[i]) \(= K\).
Hashing is appropriate only for sets (no duplicates).
Good for both in-memory and disk-based applications.
Answers the question “What record, if any, has key value K?”
17.10.1.3. Simple Examples¶
17.10.1.4. Collisions (1)¶
Given: hash function h with keys \(k_1\) and \(k_2\). \(\beta\) is a slot in the hash table.
If \(\mathbf{h}(k_1) = \beta = \mathbf{h}(k_2)\), then \(k_1\) and \(k_2\) have a collision at \(\beta\) under h.
- Search for the record with key \(K\):
Compute the table location \(\mathbf{h}(K)\).
Starting with slot \(\mathbf{h}(K)\), locate the record containing key \(K\) using (if necessary) a collision resolution policy.
17.10.1.5. Collisions (2)¶
- Collisions are inevitable in most applications.
Example: Among 23 people, some pair is likely to share a birthday.
17.10.1.6. Hash Functions (1)¶
A hash function MUST return a value within the hash table range.
To be practical, a hash function SHOULD evenly distribute the records stored among the hash table slots.
Ideally, the hash function should distribute records with equal probability to all hash table slots. In practice, success depends on distribution of actual records stored.
17.10.1.7. Hash Functions (2)¶
If we know nothing about the incoming key distribution, evenly distribute the key range over the hash table slots while avoiding obvious opportunities for clustering.
If we have knowledge of the incoming distribution, use a distribution-dependent hash function.
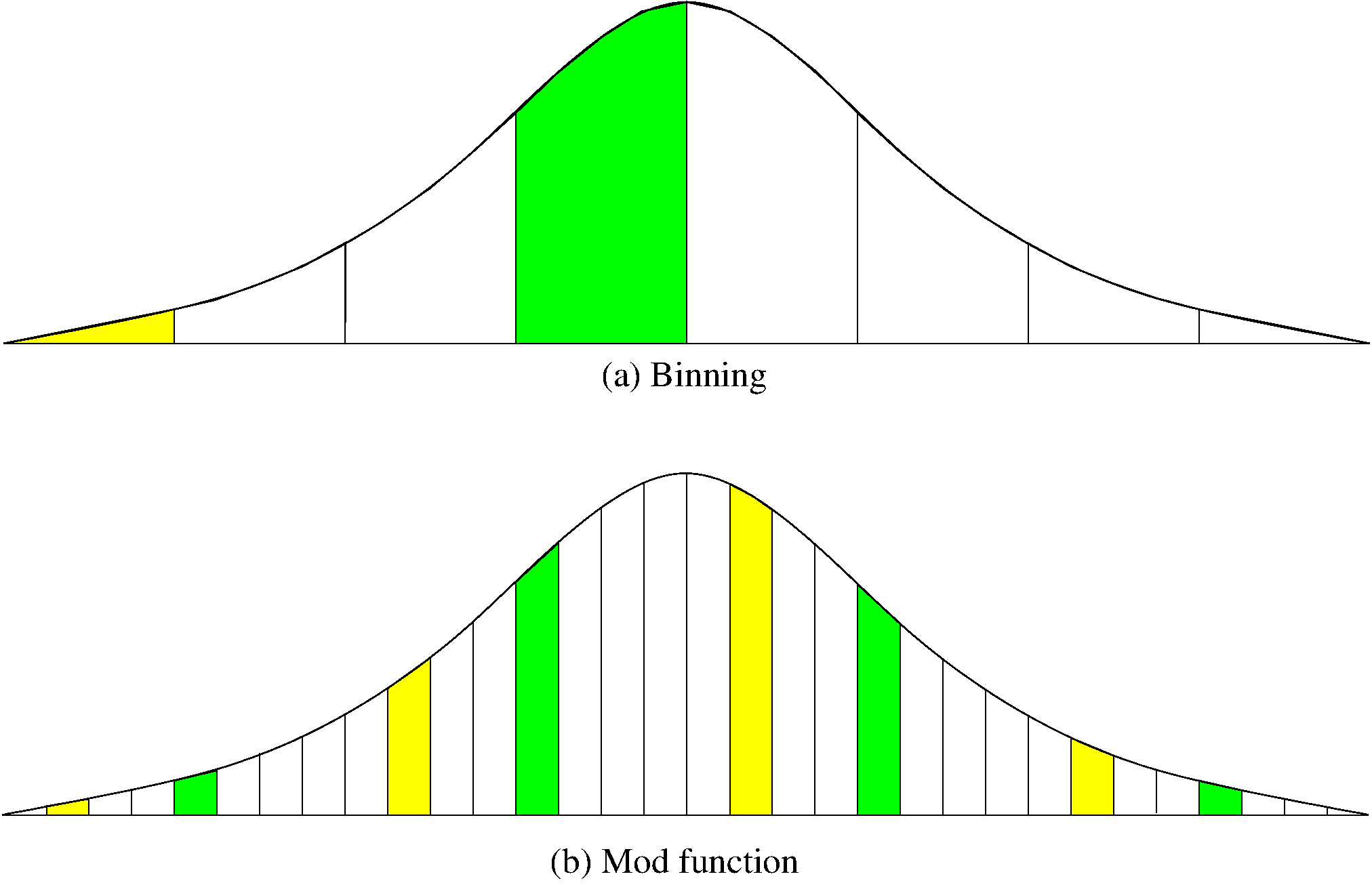
17.10.1.8. Simple Mod Function¶
17.10.1.10. Mod vs. Binning¶
17.10.1.11. Mid-Square Method¶
17.10.1.12. Strings Function: Character Adding¶
int sascii(String x, int M) { char ch[]; ch = x.toCharArray(); int xlength = x.length(); int i, sum; for (sum=0, i=0; i < x.length(); i++) sum += ch[i]; return sum % M; }
17.10.1.13. String Folding¶
// Use folding on a string, summed 4 bytes at a time int sfold(String s, int M) { long sum = 0, mul = 1; for (int i = 0; i < s.length(); i++) { mul = (i % 4 == 0) ? 1 : mul * 256; sum += s.charAt(i) * mul; } return (int)(Math.abs(sum) % M); }
17.10.1.14. Open Hashing¶
17.10.1.17. Closed Hashing¶
Closed hashing stores all records directly in the hash table.
Each record \(i\) has a home position \(\mathbf{h}(k_i)\).
If another record occupies the home position for \(i\), then another slot must be found to store \(i\).
The new slot is found by a collision resolution policy.
Search must follow the same policy to find records not in their home slots.
17.10.1.18. Collision Resolution¶
During insertion, the goal of collision resolution is to find a free slot in the table.
Probe sequence: The series of slots visited during insert/search by following a collision resolution policy.
Let \(\beta_0 = \mathbf{h}(K)\). Let \((\beta_0, \beta_1, ...)\) be the series of slots making up the probe sequence.
17.10.1.19. Insertion¶
// Insert e into hash table HT void hashInsert(const Key& k, const Elem& e) { int home; // Home position for e int pos = home = h(k); // Init probe sequence for (int i=1; EMPTYKEY != (HT[pos]).key(); i++) { pos = (home + p(k, i)) % M; // probe if (k == HT[pos].key()) { println("Duplicates not allowed"); return; } } HT[pos] = e; }
17.10.1.20. Search¶
// Search for the record with Key K bool hashSearch(const Key& K, Elem& e) const { int home; // Home position for K int pos = home = h(K); // Initial position is the home slot for (int i = 1; (K != (HT[pos]).key()) && (EMPTYKEY != (HT[pos]).key()); i++) pos = (home + p(K, i)) % M; // Next on probe sequence if (K == (HT[pos]).key()) { // Found it e = HT[pos]; return true; } else return false; // K not in hash table }
17.10.1.21. Probe Function¶
Look carefully at the probe function p():
pos = (home + p(k, i)) % M; // probeEach time p() is called, it generates a value to be added to the home position to generate the new slot to be examined.
\(p()\) is a function both of the element’s key value, and of the number of steps taken along the probe sequence. Not all probe functions use both parameters.
17.10.1.22. Linear Probing (1)¶
Use the following probe function:
p(K, i) = i;Linear probing simply goes to the next slot in the table.
Past bottom, wrap around to the top.
To avoid infinite loop, one slot in the table must always be empty.
17.10.1.24. Problem with Linear Probing¶
17.10.1.25. Linear Probing by Steps (1)¶
17.10.1.26. Linear Probing by Steps (2)¶
17.10.1.29. Quadratic Probing¶
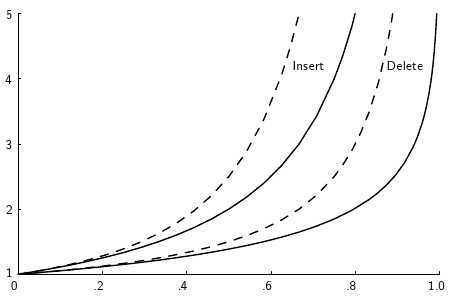
17.10.1.32. Analysis of Closed Hashing¶
The load factor is \(\alpha = N/M\) where \(N\) is the number of records currently in the table.
17.10.1.33. Deletion¶
Deleting a record must not hinder later searches.
We do not want to make positions in the hash table unusable because of deletion.
Both of these problems can be resolved by placing a special mark in place of the deleted record, called a tombstone.
A tombstone will not stop a search, but that slot can be used for future insertions.
17.10.1.35. Tombstones (2)¶
Unfortunately, tombstones add to the average path length.
- Solutions:
Local reorganizations to try to shorten the average path length.
Periodically rehash the table (by order of most frequently accessed record).
