17.9. Graphs¶
17.9.1. Graphs¶
17.9.1.1. Graphs¶
A graph \(G = (V, E)\) consists of a set of vertices \(V\), and a set of edges \(E\), such that each edge in \(E\) is a connection between a pair of vertices in \(V\).
The number of vertices is written \(|V|\), and the number edges is written \(|E|\).
17.9.1.2. Paths, Cycles¶
17.9.1.3. Connected Components¶
The maximum connected subgraphs of an undirected graph are called connected components.
17.9.1.4. Directed Graph Representation¶
17.9.1.5. Undirected Graph Representation¶
17.9.1.6. Representation Space Costs¶
- Adjacency Matrix Space:
\(|V|^2\)
Small constants
- Adjacency List Space:
\(|V| + |E|\)
Larger constants
17.9.1.7. Graph ADT¶
interface Graph { // Graph class ADT // Initialize the graph with some number of vertices void init(int n); // Return the number of vertices int nodeCount(); // Return the current number of edges int edgeCount(); // Get the value of node with index v Object getValue(int v); // Set the value of node with index v void setValue(int v, Object val); // Adds a new edge from node v to node w with weight wgt void addEdge(int v, int w, int wgt); // Get the weight value for an edge int weight(int v, int w); // Removes the edge from the graph. void removeEdge(int v, int w); // Returns true iff the graph has the edge boolean hasEdge(int v, int w); // Returns an array containing the indicies of the neighbors of v int[] neighbors(int v); }
17.9.1.8. .¶
.
17.9.1.9. Visiting Neighbors¶
int[] nList = G.neighbors(v); for (int i=0; i< nList.length; i++) { if (G.getValue(nList[i]) != VISITED) { DoSomething(); } }
17.9.1.10. Graph Traversals¶
Some applications require visiting every vertex in the graph exactly once.
The application may require that vertices be visited in some special order based on graph topology.
- Examples:
Artificial Intelligence Search
Shortest paths problems
17.9.1.11. Graph Traversals (2)¶
To insure visiting all vertices:
static void graphTraverse(Graph G) { int v; for (v=0; v<G.nodeCount(); v++) { G.setValue(v, null); // Initialize } for (v=0; v<G.nodeCount(); v++) { if (G.getValue(v) != VISITED) { doTraversal(G, v); } } }
17.9.1.12. Depth First Search (1)¶
static void DFS(Graph G, int v) { PreVisit(G, v); G.setValue(v, VISITED); int[] nList = G.neighbors(v); for (int i=0; i< nList.length; i++) { if (G.getValue(nList[i]) != VISITED) { DFS(G, nList[i]); } } PostVisit(G, v); }
17.9.1.14. Depth First Search (3)¶
Cost: \(\Theta(|V| + |E|)\).
17.9.1.15. Breadth First Search (1)¶
- Like DFS, but replace stack with a queue.
Visit vertex’s neighbors before continuing deeper in the tree.
static void BFS(Graph G, int v) { LQueue Q = new LQueue(G.nodeCount()); Q.enqueue(v); G.setValue(v, VISITED); while (Q.length() > 0) { // Process each vertex on Q v = (Integer)Q.dequeue(); PreVisit(G, v); int[] nList = G.neighbors(v); for (int i=0; i< nList.length; i++) { if (G.getValue(nList[i]) != VISITED) { // Put neighbors on Q G.setValue(nList[i], VISITED); Q.enqueue(nList[i]); } } PostVisit(G, v); } }
17.9.1.17. Topological Sort¶
Problem: Given a set of jobs, courses, etc., with prerequisite constraints, output the jobs in an order that does not violate any of the prerequisites.
17.9.1.18. Depth-First Topological Sort (1)¶
static void topsortDFS(Graph G) { int v; for (v=0; v<G.nodeCount(); v++) { G.setValue(v, null); // Initialize } for (v=0; v<G.nodeCount(); v++) { if (G.getValue(v) != VISITED) { tophelp(G, v); } } } static void tophelp(Graph G, int v) { G.setValue(v, VISITED); int[] nList = G.neighbors(v); for (int i=0; i< nList.length; i++) { if (G.getValue(nList[i]) != VISITED) { tophelp(G, nList[i]); } } printout(v); }
17.9.1.20. .¶
.
17.9.1.21. Queue-Based Topsort (1)¶
static void topsortBFS(Graph G) { // Topological sort: Queue Queue Q = new LQueue(G.nodeCount()); int[] Count = new int[G.nodeCount()]; int[] nList; int v; for (v=0; v<G.nodeCount(); v++) { Count[v] = 0; } // Initialize for (v=0; v<G.nodeCount(); v++) { // Process every edge nList = G.neighbors(v); for (int i=0; i< nList.length; i++) { Count[nList[i]]++; // Add to v's prereq count } } for (v=0; v<G.nodeCount(); v++) { // Initialize Queue if (Count[v] == 0) { // V has no prerequisites Q.enqueue(v); } } while (Q.length() > 0) { // Process the vertices v = (Integer)Q.dequeue(); printout(v); // PreVisit for Vertex V nList = G.neighbors(v); for (int i=0; i< nList.length; i++) { Count[nList[i]]--; // One less prerequisite if (Count[nList[i]] == 0) { // This vertex is now free Q.enqueue(nList[i]); } } } }
17.9.1.22. .¶
.
17.9.1.24. .¶
.
17.9.1.25. Shortest Paths Problems¶
Input: A graph with weights or costs associated with each edge.
Output: The list of edges forming the shortest path.
- Sample problems:
Find shortest path between two named vertices
Find shortest path from S to all other vertices
Find shortest path between all pairs of vertices
Will actually calculate only distances.
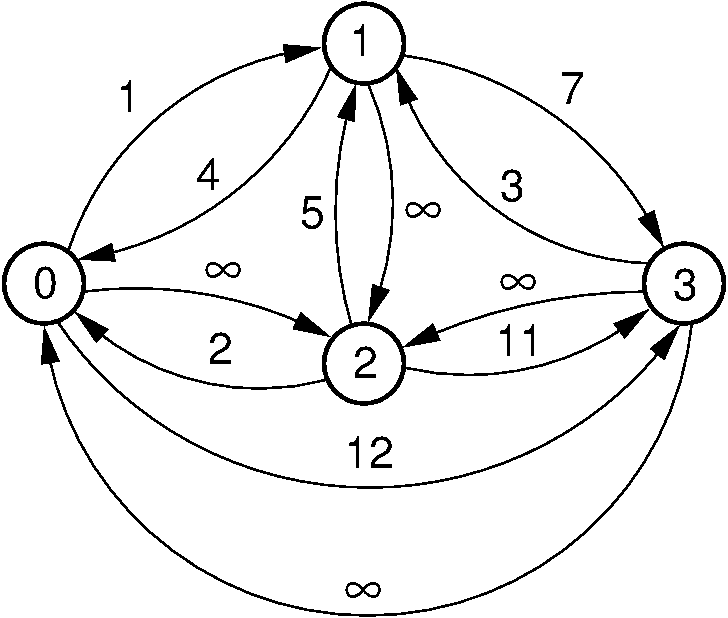
17.9.1.26. Shortest Paths Definitions¶
\(d(A, B)\) is the shortest distance from vertex \(A\) to \(B\).
\(w(A, B)\) is the weight of the edge connecting \(A\) to \(B\).
If there is no such edge, then \(w(A, B) = \infty\).
17.9.1.27. Single-Source Shortest Paths¶
Given start vertex \(s\), find the shortest path from \(s\) to all other vertices.
Try 1: Visit vertices in some order, compute shortest paths for all vertices seen so far, then add shortest path to next vertex \(x\).
Problem: Shortest path to a vertex already processed might go through \(x\).
Solution: Process vertices in order of distance from \(s\).
17.9.1.29. .¶
.
17.9.1.30. Dijkstra’s Implementation¶
// Compute shortest path distances from s, store them in D static void Dijkstra(Graph G, int s, int[] D) { for (int i=0; i<G.nodeCount(); i++) { // Initialize D[i] = INFINITY; } D[s] = 0; for (int i=0; i<G.nodeCount(); i++) { // Process the vertices int v = minVertex(G, D); // Find next-closest vertex G.setValue(v, VISITED); if (D[v] == INFINITY) { return; } // Unreachable int[] nList = G.neighbors(v); for (int j=0; j<nList.length; j++) { int w = nList[j]; if (D[w] > (D[v] + G.weight(v, w))) { D[w] = D[v] + G.weight(v, w); } } } }
17.9.1.31. Implementing minVertex¶
Issue: How to determine the next-closest vertex? (I.e., implement
minVertex)
- Approach 1: Scan through the table of current distances.
Cost: \(\Theta(|V|^2 + |E|) = \Theta(|V|^2)\).
Approach 2: Store unprocessed vertices using a min-heap to implement a priority queue ordered by \(D\) value. Must update priority queue for each edge.
Cost: \(\Theta((|V| + |E|)log|V|)\)
17.9.1.32. Approach 1¶
// Find the unvisited vertex with the smalled distance static int minVertex(Graph G, int[] D) { int v = 0; // Initialize v to any unvisited vertex; for (int i=0; i<G.nodeCount(); i++) { if (G.getValue(i) != VISITED) { v = i; break; } } for (int i=0; i<G.nodeCount(); i++) { // Now find smallest value if ((G.getValue(i) != VISITED) && (D[i] < D[v])) { v = i; } } return v; }
17.9.1.33. Approach 2¶
// Dijkstra's shortest-paths: priority queue version static void DijkstraPQ(Graph G, int s, int[] D) { int v; // The current vertex KVPair[] E = new KVPair[G.edgeCount()]; // Heap for edges E[0] = new KVPair(0, s); // Initial vertex MinHeap H = new MinHeap(E, 1, G.edgeCount()); for (int i=0; i<G.nodeCount(); i++) { // Initialize distance D[i] = INFINITY; } D[s] = 0; for (int i=0; i<G.nodeCount(); i++) { // For each vertex KVPair temp = (KVPair)(H.removemin()); if (temp == null) { return; } // Unreachable nodes exist v = (Integer)temp.value(); while (G.getValue(v) == VISITED) { temp = (KVPair)(H.removemin()); if (temp == null) { return; } // Unreachable nodes exist v = (Integer)temp.value(); } G.setValue(v, VISITED); if (D[v] == INFINITY) { return; } // Unreachable int[] nList = G.neighbors(v); for (int j=0; j<nList.length; j++) { int w = nList[j]; if (D[w] > (D[v] + G.weight(v, w))) { // Update D D[w] = D[v] + G.weight(v, w); H.insert(new KVPair(D[w], w)); } } } }
17.9.1.34. .¶
.
17.9.1.35. All-pairs Shortest Paths (1)¶
We could run Shortest Paths starting at each vertex.
- Better is to use Floyd’s algorithm.
An example of Dynamic Programming
Simpler than it sounds: A trivial triple loop
Define a k-path from vertex \(v\) to vertex \(u\) to be any path whose intermediate vertices (aside from \(v\) and \(u\)) all have indices less than \(k\).
17.9.1.36. All-pairs Shortest Paths (2)¶
17.9.1.37. Floyd’s Algorithm¶
/** Compute all-pairs shortest paths */ static void Floyd(Graph G, int[][] D) { for (int i=0; i<G.n(); i++) { // Initialize D with weights for (int j=0; j<G.n(); j++) { if (G.weight(i, j) != 0) { D[i][j] = G.weight(i, j); } } } for (int k=0; k<G.n(); k++) { // Compute all k paths for (int i=0; i<G.n(); i++) { for (int j=0; j<G.n(); j++) { if ((D[i][k] != Integer.MAX_VALUE) && (D[k][j] != Integer.MAX_VALUE) && (D[i][j] > (D[i][k] + D[k][j]))) { D[i][j] = D[i][k] + D[k][j]; } } } } }
17.9.1.38. Minimal Cost Spanning Trees¶
Minimal Cost Spanning Tree (MST) Problem:
Input: An undirected, connected graph G.
- Output: The subgraph of G that
has minimum total cost as measured by summing the values of all the edges in the subset, and
keeps the vertices connected.
17.9.1.39. MST Example¶
17.9.1.41. .¶
.
17.9.1.42. Implementation 1¶
// Compute shortest distances to the MCST, store them in D. // V[i] will hold the index for the vertex that is i's parent in the MCST void Prim(Graph G, int s, int[] D, int[] V) { for (int i=0; i<G.nodeCount(); i++) { // Initialize D[i] = INFINITY; } D[s] = 0; for (int i=0; i<G.nodeCount(); i++) { // Process the vertices int v = minVertex(G, D); // Find next-closest vertex G.setValue(v, VISITED); if (D[v] == INFINITY) { return; } // Unreachable if (v != s) { AddEdgetoMST(V[v], v); } int[] nList = G.neighbors(v); for (int j=0; j<nList.length; j++) { int w = nList[j]; if (D[w] > G.weight(v, w)) { D[w] = G.weight(v, w); V[w] = v; } } } }
17.9.1.43. Alternate Implementation¶
As with Dijkstra’s algorithm, the key issue is determining which vertex is next closest.
As with Dijkstra’s algorithm, the alternative is to use a priority queue.
Running times for the two implementations are identical to the corresponding Dijkstra’s algorithm implementations.
17.9.1.44. Kruskal’s MST Algorithm (1)¶
Initially, each vertex is in its own MST.
- Merge two MST’s that have the shortest edge between them.
Use a priority queue to order the unprocessed edges. Grab next one at each step.
How to tell if an edge connects two vertices already in the same MST?
- Use the UNION/FIND algorithm with parent-pointer
representation.
17.9.1.46. .¶
.
17.9.1.47. Kruskal’s MST Algorithm (3)¶
- Cost is dominated by the time to remove edges from the heap.
Can stop processing edges once all vertices are in the same MST
Total cost: \(\Theta(|V| + |E| log |E|)\).