8.3.1. Hard Problems¶

There are several ways that a problem could be considered hard. For example, we might have trouble understanding the definition of the problem itself. At the beginning of a large data collection and analysis project, developers and their clients might have only a hazy notion of what their goals actually are, and need to work that out over time. For other types of problems, we might have trouble finding or understanding an algorithm to solve the problem. Understanding spoken English and translating it to written text is an example of a problem whose goals are easy to define, but whose solution is not easy to discover. But even though a natural language processing algorithm might be difficult to write, the program's running time might be fairly fast. There are many practical systems today that solve aspects of this problem in reasonable time.

None of these is what is commonly meant when a computer theoretician uses the word "hard". Throughout this section, "hard" means that the best-known algorithm for the problem is expensive in its running time. One example of a hard problem is Towers of Hanoi. It is easy to understand this problem and its solution. It is also easy to write a program to solve this problem. But, it takes an extremely long time to run for any "reasonably" large value of \(n\). Try running a program to solve Towers of Hanoi for only 30 disks!

The Towers of Hanoi problem takes exponential time, that is, its running time is \(\Theta(2^n)\). This is radically different from an algorithm that takes \(\Theta(n \log n)\) time or \(\Theta(n^2)\) time. It is even radically different from a problem that takes \(\Theta(n^4)\) time. These are all examples of polynomial running time, because the exponents for all terms of these equations are constants. If we buy a new computer that runs twice as fast, the size of problem with complexity \(\Theta(n^4)\) that we can solve in a certain amount of time is increased by the fourth root of two. In other words, there is a multiplicative factor increase, even if it is a rather small one. This is true for any algorithm whose running time can be represented by a polynomial.

Consider what happens if you buy a computer that is twice as fast and try to solve a bigger Towers of Hanoi problem in a given amount of time. Because its complexity is \(\Theta(2^n)\), we can solve a problem only one disk bigger! There is no multiplicative factor, and this is true for any exponential algorithm: A constant factor increase in processing power results in only a fixed addition in problem-solving power.

There are a number of other fundamental differences between polynomial running times and exponential running times that argues for treating them as qualitatively different. Polynomials are closed under composition and addition. Thus, running polynomial-time programs in sequence, or having one program with polynomial running time call another a polynomial number of times yields polynomial time. Also, all computers known are polynomially related. That is, any program that runs in polynomial time on any computer today, when transferred to any other computer, will still run in polynomial time.

There is a practical reason for recognizing a distinction. In practice, most polynomial time algorithms are "feasible" in that they can run reasonably large inputs in reasonable time. In contrast, most algorithms requiring exponential time are not practical to run even for fairly modest sizes of input. One could argue that a program with high polynomial degree (such as \(n^{100}\)) is not practical, while an exponential-time program with cost \(1.001^n\) is practical. But the reality is that we know of almost no problems where the best polynomial-time algorithm has high degree (they nearly all have degree four or less), while almost no exponential-time algorithms (whose cost is \((O(c^n))\) have their constant \(c\) close to one. So there is not much gray area between polynomial and exponential time algorithms in practice.

For the purposes of this Module, we define a hard algorithm to be one that runs in exponential time, that is, in \(\Omega(c^n)\) for some constant \(c > 1\). A definition for a hard problem will be presented soon.

8.3.2. The Theory of NP-Completeness¶

Imagine a magical computer that works by guessing the correct solution from among all of the possible solutions to a problem. Another way to look at this is to imagine a super parallel computer that could test all possible solutions simultaneously. Certainly this magical (or highly parallel) computer can do anything a normal computer can do. It might also solve some problems more quickly than a normal computer can. Consider some problem where, given a guess for a solution, checking the solution to see if it is correct can be done in polynomial time. Even if the number of possible solutions is exponential, any given guess can be checked in polynomial time (equivalently, all possible solutions are checked simultaneously in polynomial time), and thus the problem can be solved in polynomial time by our hypothetical magical computer. Another view of this concept is this: If you cannot get the answer to a problem in polynomial time by guessing the right answer and then checking it, then you cannot do it in polynomial time in any other way.

The idea of "guessing" the right answer to a problem—or checking all possible solutions in parallel to determine which is correct—is a called a non-deterministic choice. An algorithm that works in this manner is called a non-deterministic algorithm, and any problem with an algorithm that runs on a non-deterministic machine in polynomial time is given a special name: It is said to be a problem in NP. Thus, problems in NP are those problems that can be solved in polynomial time on a non-deterministic machine.

Not all problems requiring exponential time on a regular computer are in NP. For example, Towers of Hanoi is not in NP, because it must print out \(O(2^n)\) moves for \(n\) disks. A non-deterministic machine cannot "guess" and print the correct answer in less time.

On the other hand, consider the TRAVELING SALESMAN problem.

Figure 8.3.1 illustrates this problem. Five vertices are shown, with edges and associated costs between each pair of edges. (For simplicity Figure 8.3.1 shows an undirected graph, assuming that the cost is the same in both directions, though this need not be the case.) If the salesman visits the cities in the order ABCDEA, they will travel a total distance of 13. A better route would be ABDCEA, with cost 11. The best route for this particular graph would be ABEDCA, with cost 9.

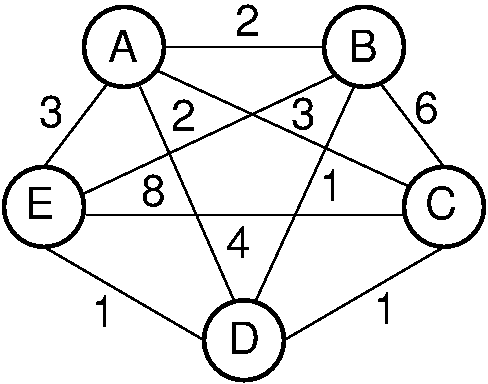
Figure 8.3.1: An illustration of the TRAVELING SALESMAN problem. Five vertices are shown, with edges between each pair of cities. The problem is to visit all of the cities exactly once, returning to the start city, with the least total cost.

We cannot solve this problem in polynomial time with a guess-and-test non-deterministic computer. The problem is that, given a candidate cycle, while we can quickly check that the answer is indeed a cycle of the appropriate form, and while we can quickly calculate the length of the cycle, we have no easy way of knowing if it is in fact the <em>shortest</em> such cycle. However, we can solve a variant of this problem cast in the form of a decision problem. A decision problem is simply one whose answer is either YES or NO. The decision problem form of TRAVELING SALESMAN is as follows.

We can solve this version of the problem in polynomial time with a non-deterministic computer. The non-deterministic algorithm simply checks all of the possible subsets of edges in the graph, in parallel. If any subset of the edges is an appropriate cycle of total length less than or equal to \(k\), the answer is YES; otherwise the answer is NO. Note that it is only necessary that some subset meet the requirement; it does not matter how many subsets fail. Checking a particular subset is done in polynomial time by adding the distances of the edges and verifying that the edges form a cycle that visits each vertex exactly once. Thus, the checking algorithm runs in polynomial time. Unfortunately, there are \(2^{|{\mathrm E}|}\) subsets to check, so this algorithm cannot be converted to a polynomial time algorithm on a regular computer. Nor does anybody in the world know of any other polynomial time algorithm to solve TRAVELING SALESMAN on a regular computer, despite the fact that the problem has been studied extensively by many computer scientists for many years.

It turns out that there is a large collection of problems with this property: We know efficient non-deterministic algorithms, but we do not know if there are efficient deterministic algorithms. At the same time, we have not been able to prove that any of these problems do not have efficient deterministic algorithms. This class of problems is called NP-complete. What is truly strange and fascinating about NP-complete problems is that if anybody ever finds the solution to any one of them that runs in polynomial time on a regular computer, then by a series of reductions, every other problem that is in NP can also be solved in polynomial time on a regular computer!

Define a problem to be NP-hard if any problem in NP can be reduced to \(X\) in polynomial time. Thus, \(X\) is as hard as any problem in NP. A problem \(X\) is defined to be NP-complete if

1. \(X\) is in NP, and
2. \(X\) is NP-hard.

The requirement that a problem be NP-hard might seem to be impossible, but in fact there are hundreds of such problems, including TRAVELING SALESMAN. Another such problem is called K-CLIQUE.

Nobody knows whether there is a polynomial time solution for K-CLIQUE, but if such an algorithm is found for K-CLIQUE or for TRAVELING SALESMAN, then that solution can be modified to solve the other, or any other problem in NP, in polynomial time.

The primary theoretical advantage of knowing that a problem P1 is NP-complete is that it can be used to show that another problem P2 is NP-complete. This is done by finding a polynomial time reduction of P1 to P2. Because we already know that all problems in NP can be reduced to P1 in polynomial time (by the definition of NP-complete), we now know that all problems can be reduced to P2 as well by the simple algorithm of reducing to P1 and then from there reducing to P2.

There is a practical advantage to knowing that a problem is NP-complete. It relates to knowing that if a polynomial time solution can be found for any problem that is NP-complete, then a polynomial solution can be found for all such problems. The implication is that,

1. Because no one has yet found such a solution, it must be difficult or impossible to do; and
2. Effort to find a polynomial time solution for one NP-complete problem can be considered to have been expended for all NP-complete problems.

How is NP-completeness of practical significance for typical programmers? Well, if your boss demands that you provide a fast algorithm to solve a problem, they will not be happy if you come back saying that the best you could do was an exponential time algorithm. But, if you can prove that the problem is NP-complete, while they still won't be happy, at least they should not be mad at you! By showing that their problem is NP-complete, you are in effect saying that the most brilliant computer scientists for the last 50 years have been trying and failing to find a polynomial time algorithm for their problem.

Problems that are solvable in polynomial time on a regular computer are said to be in class P. Clearly, all problems in P are solvable in polynomial time on a non-deterministic computer simply by neglecting to use the non-deterministic capability. Some problems in NP are NP-complete. We can consider all problems solvable in exponential time or better as an even bigger class of problems because all problems solvable in polynomial time are solvable in exponential time. Thus, we can view the world of exponential-time-or-better problems in terms of Figure 8.3.2.

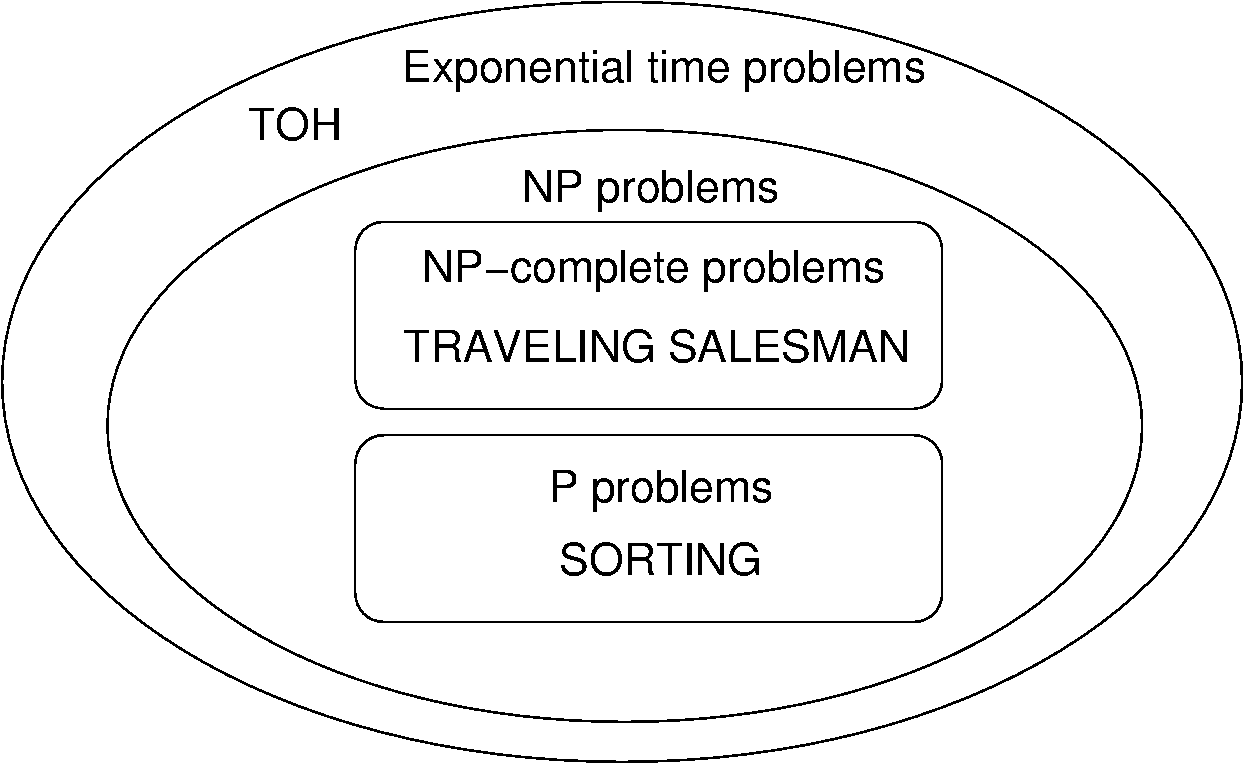
Figure 8.3.2: Our knowledge regarding the world of problems requiring exponential time or less. Some of these problems are solvable in polynomial time by a non-deterministic computer. Of these, some are known to be NP-complete, and some are known to be solvable in polynomial time on a regular computer.

The most important unanswered question in theoretical computer science is whether \(P = NP\). If they are equal, then there is a polynomial time algorithm for TRAVELING SALESMAN and all related problems. Because TRAVELING SALESMAN is known to be NP-complete, if a polynomial time algorithm were to be found for this problem, then all problems in NP would also be solvable in polynomial time. Conversely, if we were able to prove that TRAVELING SALESMAN has an exponential time lower bound, then we would know that \(P \neq NP\).