10.2. Reductions¶
10.2.1. Reductions¶
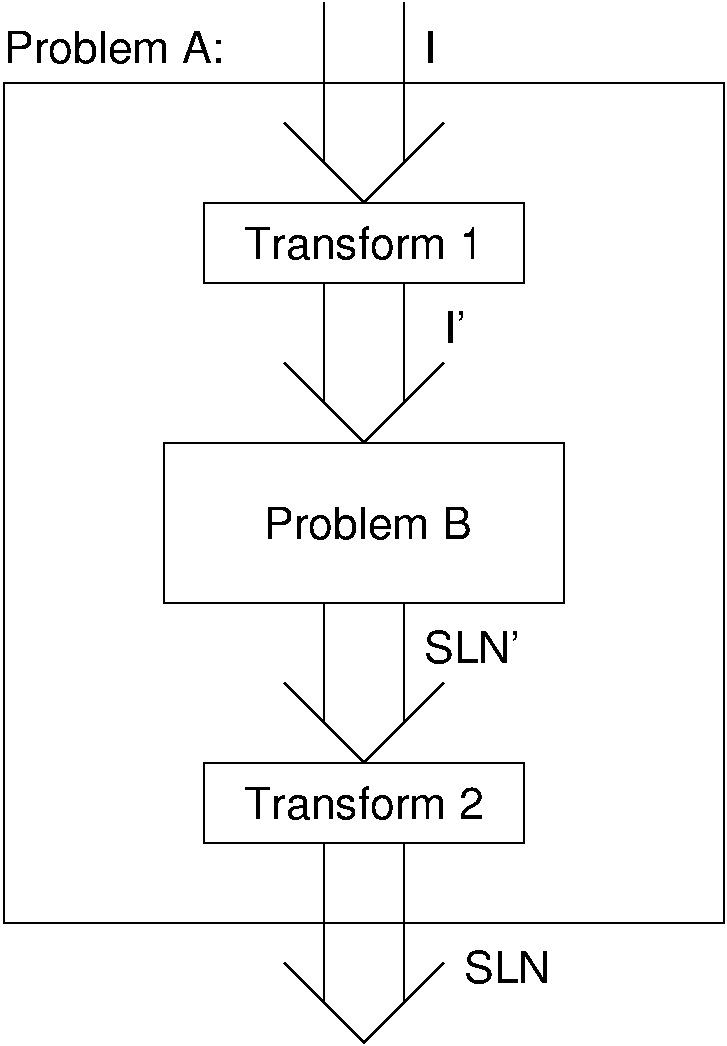
This module introduces an important concept for understanding the relationships between problems, called reduction. Reduction allows us to solve one problem in terms of another. Equally importantly, when we wish to understand the difficulty of a problem, reduction allows us to make relative statements about upper and lower bounds on the cost of a problem (as opposed to an algorithm or program).
Because the concept of a problem is discussed extensively in this chapter, we want notation to simplify problem descriptions. Throughout this chapter, a problem will be defined in terms of a mapping between inputs and outputs, and the name of the problem will be given in all capital letters. Thus, a complete definition of the sorting problem could appear as follows:
SORTING
Input: A sequence of integers \(x_0, x_1, x_2, \ldots, x_{n-1}\).
Output: A permutation \(y_0, y_1, y_2, \ldots, y_{n-1}\) of the sequence such that \(y_i \leq y_j\) whenever \(i < j\).