10.1. Parsing Introduction¶

10.1.1. Introduction¶

Parsing: Deciding if $x \in \Sigma^*$ is in $L(G)$ for some CFG $G$ .

Review: What have we done so far

Consider the CFG $G$ :

$\begin{split}\begin{eqnarray*} S &\rightarrow& Aa \\ A &\rightarrow& AA \mid ABa \mid \lambda \\ B &\rightarrow& BBa \mid b \mid \lambda \\ \end{eqnarray*}\end{split}$

Is $ba$ in $L(G)$ ? Running time?

How do you determine whether a string is in $L(G)$ ?

Note $ba$ is not in $L(G)$ for this $G$ !

Try all possible derivations, but don’t know when to stop. This runs forever!

Same grammar without lambda-rules:

Remove $\lambda$ -rules, then unit productions, and then useless productions from the grammar $G$ above. New grammar $G'$ is:

$\begin{split}\begin{eqnarray*} S &\rightarrow& Aa \mid a \\ A &\rightarrow& AA \mid ABa \mid Aa \mid Ba \mid a \\ B &\rightarrow& BBa \mid Ba \mid a \mid b \end{eqnarray*}\end{split}$

Is $ba$ in $L(G)$ ? Running time?

Note

Earlier I said this was linear time.

Try all possible derivations, there will be at most $|w|$ rounds. NOTE THIS IS NOT LINEAR TIME, IT TAKES A LONG TIME. Actual time is $|w|*p$ where $p$ is the maximum number of rules for any variable.

Note

Given grammar to represent the C Programming language, we would want to know if C programs are syntactically correct. This is one of the phases in a compiler.

Want this to run as fast as possible, don’t want to sit there and wait for your program forever to compile.

We will be looking at parsing methods that are used in writing compilers. We would like to know which rule to apply next.

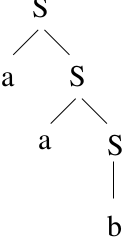
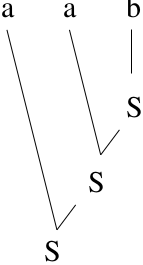
Consider string $baa$ . We would like to only try the rules that give us the derivation and ignore false paths. This would be fast! $S \Rightarrow Aa \Rightarrow Baa \Rightarrow baa$

10.1.1.1. Top-down Parser:¶

Start with $S$ and try to derive the string.

$S \rightarrow aS \mid b$
Examples: LL Parser, Recursive Descent

Bottom-up Parser:

Start with string, work backwards, and try to derive $S$ .
Examples: Shift-reduce, Operator-Precedence, LR Parser

When the grammar has a $\lambda$ -rule, it can be difficult to compute parse tables. In the example above, $A$ can disappear (due to $A \rightarrow \lambda$ ), so when $S$ is on the stack, it can be replaced by $Ac$ if either “a” or “c” are the lookahead or it can be replaced by $Bc$ if “b” is the lookahead.

We will use the following functions FIRST and FOLLOW to aid in computing parse tables.

10.1.1.2. The function FIRST¶

Some notation that we will use in defining FIRST and FOLLOW.

$G=(V, T, S, P)$

$w, v \in (V \cup T)^*$

$a \in T$

$X, A, B \in V$

$X_I \in (V \cup T)^+$

Definition: $\mbox{FIRST}(w) =$ the set of terminals that begin strings derived from $w$ .

If $w \buildrel * \over \Rightarrow av$ then

$a$ is in $\mbox{FIRST}(w)$

If $w \buildrel * \over \Rightarrow \lambda$ then

$\lambda$ is in $\mbox{FIRST}(w)$

Example from previous grammar: $\mbox{FIRST}(aAb) = \{a\}$ , since you have $aAb \Rightarrow a...b$ , and $\mbox{FIRST}(Ac) = \{a, c\}$

To compute FIRST:

$\mbox{FIRST}(a) = \{a\}$ where a is a terminal.
$\mbox{FIRST}(X)$ where $X$ is a variable.
1. If $X \rightarrow aw$ then
  
  $a$ is in $\mbox{FIRST}(X)$
2. If $X \rightarrow \lambda$ then
  
  $\lambda$ is in $\mbox{FIRST}(X)$
3. If $X \rightarrow Aw$ and $\lambda \in \mbox{FIRST}(A)$ then
  
  Everything in $\mbox{FIRST}(w)$ is in $\mbox{FIRST}(X)$
In general, $\mbox{FIRST}(X_1X_2X_3...X_K) =$
- $\mbox{FIRST}(X_1)$
- $\cup\ \mbox{FIRST}(X_2)$ if $\lambda$ is in $\mbox{FIRST}(X_1)$
- $\cup\ \mbox{FIRST}(X_3)$ if $\lambda$ is in $\mbox{FIRST}(X_1)$
  
  and $\lambda$ is in $\mbox{FIRST}(X_2)$
  
  …
- $\cup\ \mbox{FIRST}(X_K)$ if $\lambda$ is in $\mbox{FIRST}(X_1)$
  
  and $\lambda$ is in $\mbox{FIRST}(X_2)$
  
  … and $\lambda$ is in $\mbox{FIRST}(X_{K-1})$
- $-\ \{\lambda\}$ if $\lambda \notin \mbox{FIRST}(X_J)$ for all $J$
(where $X_I$ represents a terminal or a variable)

We will be computing $\mbox{FIRST}(w)$ where $w$ is the right hand side of a rule. Thus, we will need to compute $\mbox{FIRST}(X)$ for each symbol $X$ (either terminal or variable) that appears in the right hand side of a rule.

Example 10.1.1

$L = \{a^nb^mc^n : n \ge 0, 0 \le m \le 1\}$

$\begin{split}\begin{eqnarray*} S &\rightarrow& aSc \mid B \\ B &\rightarrow& b \mid \lambda\\ \end{eqnarray*}\end{split}$

$\mbox{FIRST}(B) = \{b, \lambda \}$

Using $B \rightarrow b$ gives that $b$ is in $\mbox{FIRST}(B)$ . Using $B \rightarrow \lambda$ gives that $\lambda$ is in $\mbox{FIRST}(B)$ .

$\mbox{FIRST}(S) = \{a, b, \lambda\}$

Using $S \rightarrow aSc$ gives that $a$ is in $\mbox{FIRST}(S)$ .

Using $S \rightarrow B$ and $\lambda$ is in $\mbox{FIRST}(B)$ gives that everything in $\mbox{FIRST}(B)$ is in $\mbox{FIRST}(S)$ , so $b$ and $\lambda$ are in $\mbox{FIRST}(S)$ .

$\mbox{FIRST}(Sc) = \{a, b, c\}$

Example 10.1.2

$\begin{split}\begin{eqnarray*} S &\rightarrow& BCD \mid aD \\ A &\rightarrow& CEB \mid aA\\ B &\rightarrow& b \mid \lambda\\ C &\rightarrow& dB \mid \lambda\\ D &\rightarrow& cA \mid \lambda\\ E &\rightarrow& e \mid fE\\ \end{eqnarray*}\end{split}$

Note

Why do we not calculate $\mbox{FIRST}(S)$ first?

$\mbox{FIRST}(S) = \{b, d, c, \lambda, a\}$

$\mbox{FIRST}(A) = \{d, e, f, a\}$

$\mbox{FIRST}(B) = \{b, \lambda\}$

$\mbox{FIRST}(C) = \{d, \lambda\}$

$\mbox{FIRST}(D) = \{c, \lambda\}$

$\mbox{FIRST}(E) = \{e, f\}$

10.1.1.3. The function FOLLOW¶

Definition: $\mbox{FOLLOW}(X) =$ set of terminals that can appear to the right of $X$ in some derivation. (We only compute FOLLOW for variables.)

If $S \buildrel * \over \Rightarrow wAav$ then

$a$ is in $\mbox{FOLLOW}(A)$

(where $w$ and $v$ are strings of terminals and variables, $a$ is a terminal, and $A$ is a variable)

To compute FOLLOW:

$\$$ is in $\mbox{FOLLOW}(S)$

If $A \rightarrow wBv$ and $v \ne \lambda$ then

$\mbox{FIRST}(v) - \{ \lambda \}$ is in $\mbox{FOLLOW}(B)$

If $A \rightarrow wB$ or $A \rightarrow wBv$ and $\lambda$ is in $\mbox{FIRST}(v)$ then

$\mbox{FOLLOW}(A)$ is in $\mbox{FOLLOW}(B)$

$\lambda$ is never in FOLLOW

Example 10.1.3

$S \rightarrow aSc \mid B$

$B \rightarrow b \mid \lambda$

Note

Do a sample derivation of $aabcc$ and show that $c$ follows $S$ , $c$ follows $B$ .

Reminder: $\lambda$ is never in a FOLLOW set.

$\mbox{FOLLOW}(S) = \{ \$, c \}$

$\$$ goes into $\mbox{FOLLOW}(S)$ by rule 1. Then $c$ goes into $\mbox{FOLLOW}(S)$ by rule 2 since $S \rightarrow aSc$ and $\mbox{FIRST}(c) = \{c\}$ .

$\mbox{FOLLOW}(B) = \{ \$, c \}$

By rule 3 and $S \rightarrow B$ , $\mbox{FOLLOW}(S)$ is added to $\mbox{FOLLOW}(B)$ .

Example 10.1.4

S→BCD∣aD
A→CEB∣aA
B→b∣λ
C→dB∣λ
D→cA∣λ
E→e∣fE

$\mbox{FOLLOW}(S) = \{\$\}$

$\mbox{FOLLOW}(A) = \{\$\}$

$\mbox{FOLLOW}(B) = \{d, c, e, f\$\}$

$\mbox{FOLLOW}(C) = \{c, e, f\$\}$

$\mbox{FOLLOW}(D) = \{\$\}$

$\mbox{FOLLOW}(E) = \{b, \$\}$

CS4114 Formal Languages Spring 2021

Chapter 10 Parsing

10.1. Parsing Introduction¶

10.1.1. Introduction¶

10.1.1.1. Top-down Parser:¶

10.1.1.2. The function FIRST¶

10.1.1.3. The function FOLLOW¶