4.1. Context-Free Languages¶
4.1.1. Programming Languages¶
Regular LanguagesKeywords in a programming languageNames of identifiersIntegersA finite list of miscillaneous symbols:= \ ;Non-regular Languages\(\{a^ncb^n | n > 0\}\)Expressions: \(((a + b) - c)\)Block structures (\(\{\}\) in Java/C++ andbegin…endin Pascal)(What memory would you need to recognize each of these langauges?)
4.1.2. Context Free Languages¶
Definition: A grammar \(G = (V, T, S, P)\) is context-free if all productions are of the form\(A \rightarrow x\)where \(A \in V\) and \(x \in (V \cup T)^*\).Key point: A grammar is context-free if the LHS of every rule is a single variable.
Definition: \(L\) is a context-free language (CFL) iff there exists a context-free grammar (CFG) \(G\) such that \(L = L(G)\).
4.1.3. Example¶
\(G =(\{S\}, \{a, b\}, S, P)\)\(S \rightarrow aSb\ |\ ab\)Derivation of \(aaabbb\):\(S \Rightarrow aSb \Rightarrow aaSbb \Rightarrow aaabbb\)\(L(G) = \{a^nb^n | n > 0\}\)
4.1.4. Linear Grammars¶
Definition: A linear grammar has at most one variable on the right hand side of any production. Thus, right linear and left linear grammars are also linear grammars.
But many other grammars are linear as well.
\(G = (\{S\}, \{a, b\}, S, P)\)\(S \rightarrow aSa\ |\ bSb\ |\ a\ |\ b\ |\ \lambda\)Derivation of \(ababa\): \(S \Rightarrow aSa \Rightarrow abSba \Rightarrow ababa\)\(\Sigma = \{a, b\}, L(G) = \{w \in {\Sigma}^{*} | w=w^R\}\),
4.1.5. Example¶
\(G = (\{S, A, B\}, \{a, b, c\}, S, P)\)\(S \rightarrow AcB\)\(A \rightarrow aAa\ |\ \lambda\)\(B \rightarrow Bbb\ |\ \lambda\)\(L(G) = \{a^{2n}cb^{2m} | n, m \ge 0\}\)Note this is a context-free language and also a regular language.(Even if this doesn’t happen to be a regular grammar.)
4.1.6. Example (cont)¶
Derivations of \(aacbb\):1. \(S \Rightarrow \underline{A}cB \Rightarrow a\underline{A}acB \Rightarrow aac\underline{B} \Rightarrow aac\underline{B}bb \Rightarrow aacbb\)2. \(S \Rightarrow Ac\underline{B} \Rightarrow Ac\underline{B}bb \Rightarrow \underline{A}cbb \Rightarrow a\underline{A}acbb \Rightarrow aacbb\)(Next variable to be replaced is underlined.)There are multiple derivations for this string.This grammar is not a linear grammar, as there is a choice of which variable to replace.
To write an efficient algorithm to perform replacements, we need some order.
4.1.7. Derivations¶
Definition: Leftmost derivation: in each step of a derivation, replace the leftmost variable. (See derivation 1 above.)
Definition: Rightmost derivation: in each step of a derivation, replace the rightmost variable. (See derivation 2 above.)
Derivation Trees (also known as “parse trees”): A derivation tree represents a derivation, but does not show the order in which productions were applied.
4.1.8. Example¶
A derivation tree for \(G = (V, T, S, P)\):Root is labeled \(S\)Leaves are labeled \(x\), where \(x \in T \cup \{\lambda\}\)Non-leaf vertices labeled \(A, A \in V\)For rule \(A \rightarrow a_1a_2a_3\ldots a_n\), where \(A \in V, a_i \in (T \cup V \cup \{\lambda\})\),
4.1.9. Example¶
\(G = (\{S, A, B\}, \{a, b, c\}, S, P)\)\(S \rightarrow AcB\)\(A \rightarrow aAa\ |\ \lambda\)\(B \rightarrow Bbb\ |\ \lambda\)Derivation trees do not denote the order variables are replaced!But we can get a leftmost or rightmost derivation from looking at tree.
4.1.10. Derivation Example¶
4.1.11. More on derivations¶
Definitions: Partial derivation tree - subtree of derivation tree.
If partial derivation tree has root \(S\) then it represents a sentential form.
Leaves from left to right in a derivation tree form the yield of the tree.
If \(w\) is the yield of a derivation tree, then it must be that \(w \in L(G)\).
The yield for the example above is \(aacbb\).
4.1.12. Examples¶
A partial derivation tree that has root S:
The yield of this example is \(aAacB\) (which is a sentential form).A partial derivation tree that does not have root S:
4.1.13. Membership problem (1)¶
Membership: Given CFG \(G\) and string \(w \in \Sigma^*\), is \(w \in L(G)\)?If we can find a derivation of \(w\), then we would know that \(w\) is in \(L(G)\).Motivation:\(G\) is the grammar for Java.\(w\) is your Java program.Is \(w\) syntactically correct?
This is (part of) what a compiler does. You write a program, you compile it, and the compiler finds all your syntax mistakes.
(Code generation: It also “translates” the program into “bytecode” to be executed)
4.1.14. Example¶
\(G = (\{S\}, \{a, b\}, S, P), P =\)\(S \rightarrow SS\ |\ aSa\ |\ b\ |\ \lambda\)\(L_1 = L(G) = \{w \in \Sigma^* |\ \mbox{strings with an even number of a's}\}\)Is \(abbab \in L(G)\)?Exhaustive Search AlgorithmFor all \(i = 1, 2, 3, \ldots\)Examine all sentential forms yielded by \(i\) substitutions
4.1.15. Example of Derivation (1)¶
Is \(abbab \in L(G)\)?
\(i = 1\)1. \(S \Rightarrow SS\)2. \(S \Rightarrow aSa\)3. \(S \Rightarrow b\)4. \(S \Rightarrow \lambda\)
4.1.16. Example of Derivation (2)¶
\(i=2\)1. \(S \Rightarrow SS \Rightarrow SSS\)2. \(S \Rightarrow SS \Rightarrow aSaS\)3. \(S \Rightarrow SS \Rightarrow bS\)4. \(S \Rightarrow SS \Rightarrow S\)5. \(S \Rightarrow aSa \Rightarrow aSSa\)…Note: Will we find \(w\)? How long will it take? If we just do leftmost derivations, then for \(i = 2\), 8 of length 2.When \(i = 6\) we will find the derivation of \(w\).\(S \Rightarrow SS \Rightarrow aSaS \Rightarrow aSSaS \Rightarrow abSaS \Rightarrow abba \Rightarrow abbab\)
4.1.17. Derivation: Strings Not in Language¶
Question: What happens if \(w\) is not in \(L(G)\)?When do we stop the loop in the algorithm and know for sure that \(w\) is not going to be derived? \(S \Rightarrow SS ... \Rightarrow SSSSSSSSSS ... \Rightarrow S\)Hard to determine that \(baaba\) is not in \(L(G)\). Potential infinite loops.We want to consider special forms of context free grammars such that we can determine when strings are or are not in the language.Easy to write a context-free grammar and then convert it into a special form such that it will be easier to test membership.
4.1.18. CFG Theorem (1)¶
Theorem: If CFG \(G\) does not contain rules of the form
\(A \rightarrow \lambda\qquad\) [\(\lambda\) production]\(A \rightarrow B\qquad\) [Unit production]where \(A, B \in V\), then we can determine if \(w \in L(G)\) or if \(w \not\in L(G)\).
4.1.19. CFG Theorem (2)¶
Proof: Consider
1. Length of sentential forms2. Number of terminal symbols in a sentential formEither 1 or 2 increases with each derivation.
Derivation of string \(w\) in \(L(G)\) takes \(\le 2|w|\) times through loop in the exhaustive algorithm.
Thus, if there are \(> 2|w|\) times through loop, then \(w \not\in L(G)\).
4.1.20. Example (1)¶
Let \(L_2 = L_1 - \{\lambda\}\). \(L_2 = L(G)\) where \(G\) is
\(S \rightarrow SS\ |\ aa\ |\ aSa\ |\ b\)NOTE that this grammar is in the correct form for the theorem.
Show \(baaba \not\in L(G)\).
4.1.21. Example (2)¶
\(i = 1\)1. \(S \Rightarrow SS\)2. \(S \Rightarrow aSa\)3. \(S \Rightarrow aa\)4. \(S \Rightarrow b\)
4.1.22. Example (3)¶
\(i = 2\)1. \(S \Rightarrow SS \Rightarrow SSS\)2. \(S \Rightarrow SS \Rightarrow aSaS\)3. \(S \Rightarrow SS \Rightarrow aaS\)4. \(S \Rightarrow SS \Rightarrow bS\)5. \(S \Rightarrow aSa \Rightarrow aSSa\)6. \(S \Rightarrow aSa \Rightarrow aaSaa\)7. \(S \Rightarrow aSa \Rightarrow aaaa\)8. \(S \Rightarrow aSa \Rightarrow aba\)
4.1.23. Example (4)¶
With each substitution, either there is at least one more terminal or the length of the sentential form has increased.
So after we process the loop for \(i = 10\), we can conclude that \(baaba\) is not in \(L(G)\).
4.1.24. Not all grammars considered equal¶
Later, we will learn methods for taking a grammar and transforming it into an equivalent (or almost) equivalent grammar.
For now, here is another form that will make membership testing easier.
Definition: Simple grammar (or s-grammar) has all productions of the form:\(A \rightarrow ax\)where \(A \in V\), \(a \in T\), and \(x \in V^*\) AND any pair \((A, a)\) can occur in at most one rule.If you use the exhaustive search method to ask if \(w \in L(G)\), where \(G\) is an s-grammar, the number of terminals increases with each step.Q: Why is this not a right-linear grammar? (And so what if it was?)
4.1.25. Ambiguity¶
Definition: A CFG \(G\) is ambiguous if there exists some \(w \in L(G)\) which has two distinct derivation trees.
4.1.26. Ambiguity Example (1)¶
Expression grammar
\(G = (\{E, I\}, \{a, b, +, *, (, )\}, E, P), P =\)
\(E \rightarrow E+E\ |\ E*E\ |\ (E)\ |\ I\)\(I \rightarrow a\ |\ b\)Derivation of \(a+b*a\) is:
\(E \Rightarrow \underline{E}+E \Rightarrow \underline{I}+E \Rightarrow a+\underline{E} \Rightarrow a+\underline{E}*E \Rightarrow a+\underline{I}*E \Rightarrow a+b*\underline{E} \Rightarrow a+b*\underline{I} \Rightarrow a+b*a\)
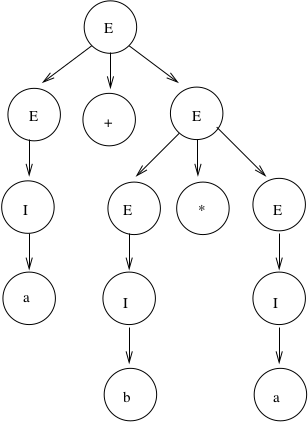
4.1.27. Ambiguity Example (2)¶
4.1.28. Ambiguity Example (3)¶
Another derivation of \(a+b*a\) is:\(E \Rightarrow \underline{E}*E \Rightarrow \underline{E}+E*E \Rightarrow \underline{I}+E*E \Rightarrow a+\underline{E}*E \Rightarrow a+\underline{I}*E \Rightarrow a+b*\underline{E} \Rightarrow a+b*\underline{I} \Rightarrow a+b*a\)Corresponding derivation tree is: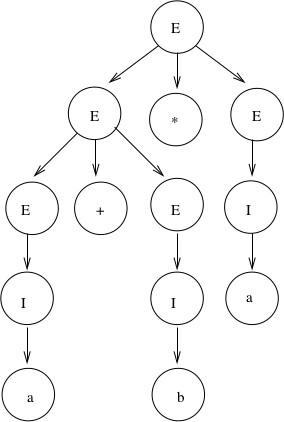
If \(a = 2\) and \(b = 4\), then the “result” of this expression is \((2+4)*2 = 12\).
4.1.29. Ambiguity Example (3)¶
There are two distinct derivation trees for the same string. Thus the grammar is ambiguous. The string can have different meanings depending on which way it is interpreted.
If \(G\) is a grammar for Java programs and \(w\) is Bob’s Java program, he doesn’t want one compiler to give one meaning to his program and another compiler to interpret his program differently. Disaster!
4.1.30. Rewriting the Grammar (1)¶
Rewrite the grammar as an unambiguous grammar. (Specifically, with the meaning that multiplication has higher precedence than addition.)
\(E \rightarrow E+T\ |\ T\)\(T \rightarrow T*F\ |\ F\)\(F \rightarrow I\ |\ (E)\)\(I \rightarrow a\ |\ b\)
4.1.31. Rewriting the Grammar (2)¶
4.1.32. .¶
.
4.1.33. Rewriting the Grammar (3)¶
Try to get a derivation tree with the other meaning of \(a+b*c\), when \(*\) is closer to the root of the tree.
\(E \Rightarrow T \Rightarrow T*F ...\) Then the only way to include a “\(+\)” before the multiplication is if the addition is enclosed in parenthesis. Thus, there is only one meaning that is accepted.
4.1.34. Unambiguous Grammars¶
Definition: If \(L\) is CFL and \(G\) is an unambiguous CFG such that \(L = L(G)\), then \(L\) is unambiguous.
<<Why are we studying CFL? Because we want to be able to represent syntactically correct programs.>>
4.1.35. Backus-Naur Form of a grammar:¶
Nonterminals are enclosed in brackets \(<>\)For “\(\rightarrow\)” use instead “\(::=\)”Sample C++ Program::
main () { int a; int b; int sum; a = 40; b = 6; sum = a + b; cout << "sum is "<< sum << endl; }
4.1.36. Programming Language (1)¶
“Attempt” to write a CFG for C++ in BNF (Note: \(<\mbox{program}>\) is start symbol of grammar:
<program> ::= main () <block> <block> ::= { <stmt-list> } <stmt-list> ::= <stmt> | <stmt> stmt-list> | <decl> | <decl> <stmt-list> <decl> ::= int <id> ; | double <id> ; <stmt> ::= <asgn-stmt> | <assgn-stmt> | <cout-stmt> <asgn-stmt> ::= <id> = <expr> ; <expr> ::= <expr> + <expr> | <expr> * <expr> | ( <expr> ) | <id> <cout-stmt> ::= cout <out-list>etc., Must expand all nonterminals!
4.1.37. Programming Language (2)¶
So a derivation of the program test would look like:
<program> ==> main() <block> ==> main() { <stmt-list> } ==> main() { <decl> <stmt-list> } ==> main() { int <id> <stmt-list> } ==> main() { int a <stmt-list> } ... ==> complete C++ program
4.1.38. Limits to CFG¶
Can write a CFG that recognizes all syntactically correct programs.Problem: The CFG also accepts incorrect programs.Can’t recognize errors like:Declare the same variable twice, once as an integer and once as a char.Assign a real value to a character.We can write a CFG \(G\) such that \(L(G) = \{ \mbox{syntactically correct C++ programs} \}\).But \(\{ \mbox{semantically correct C++ programs} \} \subset L(G)\).Example: Formal parameters should match actual parameters (# and type):
declare: int Sum(int a, int b, int c) ... call: newsum = Sum(x,y);