Context-Free Languages¶
1. Context-Free Languages¶
In the previous chapters, we see that some languages are regular languages, which means that we can define a DFA, NFA, Regular expression, or Regular grammar for them.
Examples of regular languages:
keywords in a programming language
names of identifiers
integers
a finite list of miscillaneous symbols: = ;
Then we covered the Pumping Lemma which is a tool to prove that if a language is not regular.
Examples for Not Regular languages:
expressions: \(((a + b) - c)\)
block structures (\(\{\}\) in Java/C++ and
begin…endin Pascal)
We know that not all languages are not regular, since we’ve proved some are not. Now we will look at a class of languages that is larger than the regular languages, and more powerful: Context-free languages.
Definition: A grammar \(G = (V, T, S, P)\) is context-free if all productions are of the form
\(A \rightarrow x\)
Definition: \(L\) is a context-free language (CFL) iff \(\exists\) context-free grammar (CFG) \(G\) such that \(L = L(G)\).
The above definition for Grammars is exactly the same as the one we keep using from the first chapter in this book. This means that all grammars we used (including the Regular Grammars) are Context Free Grammars.
Example 1
Note
We have seen this before! It’s not regular!
Definition: A linear grammar has at most one variable on the right hand side of any production. Thus, right linear and left linear grammars are also linear grammars.
So, this is a linear grammar.
Example 2
Definition: String derivation is to start at the starting point of the grammar and do replacements until you can do no more replacements. A variable in the grammar can be replaced by the right hand side of its rule
Example 3
This grammar is not a linear grammar, as there is a choice of which variable to replace.
By looking at the previous example, some sentential forms have multiple variables, this raises a question, Which variable should be replaced? To write an algorithm to perform replacements, we need some order. We will see this when we look at parsing algorithms.
Definition: Leftmost derivation: in each step of a derivation, replace the leftmost variable. (See derivation 1 above).
Definition: Rightmost derivation: in each step of a derivation, replace the rightmost variable. (See derivation 2 above).
Derivation Trees (also known as “parse trees”): A derivation tree represents a derivation, but does not show the order in which productions were applied.
Example 4
A derivation tree for \(G = (V, T, S, P)\):
root is labeled \(S\)
leaves are labeled \(x\), where \(x \in T \cup \{\lambda\}\)
nonleaf vertices labeled \(A, A \in V\)
For rule \(A \rightarrow a_1a_2a_3\ldots a_n\), where \(A \in V, a_i \in (T \cup V \cup \{\lambda\})\),
Example 5
NOTE: Derivation trees do not define an order in which variables are replaced! We could however get a leftmost or rightmost derivation easily from looking at the tree.
Note
Question: What string is this?
Answer: aacbb
Question: Describe the language that this grammar produces.
Answer: Zero or more pairs of a’s followed by c followed by zero or more pairs of b’s.
Question: What if we want the same number of a’s and b’s?
Answer: S -> c | aaSbb
Let us see an example for how the previous parse tree was built.
Definitions: Partial derivation tree - subtree of derivation tree.
If partial derivation tree has root \(S\) then it represents a sentential form.
Leaves from left to right in a derivation tree form the yield of the tree.
If \(w\) is the yield of a derivation tree, then it must be that \(w \in L(G)\).
The yield for the example above is \(aacbb\).
Example 6
A partial derivation tree that has root S (so it is a sentential form):
The yield for this example is \(aAacB\).
Example 7
A partial derivation tree that does not have root S:
Membership: Given CFG \(G\) and string \(w \in \Sigma^*\), is \(w \in L(G)\)?
If we can find a derivation of \(w\), then we would know that \(w\) is in \(L(G)\).
Why would anybody want to do this? Consider the case where \(G\) is a grammar for Java, and \(w\) is a Java program. Is \(w\) a syntactically correct program? This is (part of) what a compiler does. You write a program, you compile it, and the compiler finds all your syntax mistakes. (It also “translates” the program into “bytecode” to be executed. We won’t talk much about that aspect of compilers in this class.)
Example 8
Exhaustive Search Algorithm
If you were to run this in OpenFLAP, it takes a LONG time, but eventually accepts. The problem is that this approach is rather inefficient since it is using an exhaustive search for all ways of expanding from the start symbol.
For all \(i = 1, 2, 3, \ldots\)Examine all sentential forms yielded by \(i\) substitutions
Example 9
Is \(abbab \in L(G)\)?
Note: Will we find \(w\)? How long will it take? If we just do leftmost derivations, then for \(i = 2\), 8 of length 2.
When \(i = 6\) we will find the derivation of \(w\).
\(S \Rightarrow SS \Rightarrow aSaS \Rightarrow aSSaS \Rightarrow abSaS \Rightarrow abba \Rightarrow abbab\)
Question: What happens if \(w\) is not in \(L(G)\)? When do we stop the loop in the algorithm and know for sure that \(w\) is not going to be derived? \(S \Rightarrow SS \Rightarrow ... \Rightarrow SSSSSSSSSS \Rightarrow ...\) This process cannot determine that \(baaba\) is not in \(L(G)\).
We want to consider special forms of context free grammars such that we can determine when strings are or are not in the language. It turns out to be easy take a context-free grammar and convert it into a special form that makes it easier to test membership.
Theorem 1
Theorem: If CFG \(G\) does not contain rules of the form
\(A \rightarrow \lambda\)\(A \rightarrow B\)
where \(A, B \in V\), then we can determine if \(w \in L(G)\) or if \(w \not\in L(G)\).
Proof: Consider
1. length of sentential forms2. number of terminal symbols in a sentential form
Either 1 or 2 increases with each derivation.
Derivation of string \(w\) in \(L(G)\) takes \(\le 2|w|\) times through loop in the exhaustive algorithm.
Thus, if there are \(> 2|w|\) times through loop, then \(w \not\in L(G)\).
Example 10
Let \(L_2 = L_1 - \{\lambda\}\). \(L_2 = L(G)\) where \(G\) is:
\(S \rightarrow SS\ |\ aa\ |\ aSa\ |\ b\)
NOTE that this grammar is in the correct form for the theorem.
Show \(baaba \not\in L(G)\).
With each substitution, either there is at least one more terminal or the length of the sentential form has increased.
So after we process the loop for \(i = 10\), we can conclude that \(baaba\) is not in \(L(G)\).
Next chapter, we will learn methods for taking a grammar and transforming it into an equivalent (or almost equivalent) grammar. We will see that some ways of writing a grammar for a language are better than others, in terms of our ability to write practical algorithms for solving the membership problem. For now, here is another form that will make membership testing easier.
Definition: Simple grammar (or s-grammar) has all productions of the form:
\(A \rightarrow ax\)
where \(A \in V\), \(a \in T\), and \(x \in V^*\) AND any pair \((A, a)\) can occur in at most one rule.
If you use the exhaustive search method to ask if \(w \in L(G)\), where \(G\) is an s-grammar, the number of terminals increases with each step.
2. Ambiguity¶
Definition: A CFG \(G\) is ambiguous if \(\exists\) some \(w \in L(G)\) which has two distinct derivation trees.
Example 11
Expression grammar
\(G = (\{E, I\}, \{a, b, +, *, (, )\}, E, P), P =\)
\(E \rightarrow E+E\ |\ E*E\ |\ (E)\ |\ I\)\(I \rightarrow a\ |\ b\)
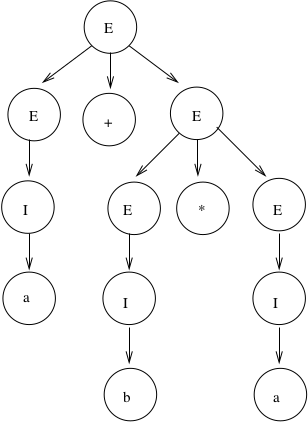
Derivation of \(a+b*a\) is:
\(E \Rightarrow \underline{E}+E \Rightarrow \underline{I}+E \Rightarrow a+\underline{E} \Rightarrow a+\underline{E}*E \Rightarrow a+\underline{I}*E \Rightarrow a+b*\underline{E} \Rightarrow a+b*\underline{I} \Rightarrow a+b*a\)
Corresponding derivation tree is:
Derivation trees of expressions are evaluated bottom up. So if \(a = 2\) and \(b = 4\), then the “result” of this expression is \(2+(4*2) = 10\).
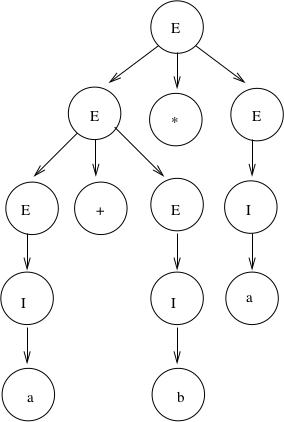
Another derivation of \(a+b*a\) is:
\(E \Rightarrow \underline{E}*E \Rightarrow \underline{E}+E*E \Rightarrow \underline{I}+E*E \Rightarrow a+\underline{E}*E \Rightarrow a+\underline{I}*E \Rightarrow a+b*\underline{E} \Rightarrow a+b*\underline{I} \Rightarrow a+b*a\)
Corresponding derivation tree is:
If \(a = 2\) and \(b = 4\), then the “result” of this expression is \((2+4)*2 = 12\).
There are two distinct derivation trees for the same string. Thus the grammar is ambiguous. The string can have different meanings depending on which way it is interpreted.
If \(G\) is a grammar for Java programs and \(w\) is Bob’s Java program, he doesn’t want one compiler to give one meaning to his program and another compiler to interpret his program differently. Disaster!
Definition: If \(L\) is CFL and \(G\) is an unambiguous CFG such that \(L = L(G)\), then \(L\) is unambiguous.
Note
Why are we studying CFL? Because we want to be able to represent syntactically correct programs.
The review problem set for this module contains four review problems, the first three of which refer to the same grammar. The first problem is about determining how many parse trees a given string has in a given grammar.
2.1. Ambiguous Grammars (2)¶
This problem is again about determining how many parse trees a given string has in a given grammar.
2.2. Ambiguous Grammars (3)¶
This problem is once more about determining how many parse trees a given string has in a given grammar.
2.3. Ambiguous Grammars (4)¶
This problem will help you discover ambiguities in grammars as well as convince yourself that a grammar is not ambiguous.
3. Eliminating Grammar Ambiguity¶
In general, there is no universal solution to eliminate grammar ambiguity. However, based on the grammar on hand, there are some tricks that can help to eliminate the amibuity. These common tricks are:
Operator precedence
Operator associativity
Rewrite the grammar from scratch
3.1. Precedence¶
By looking at the grammar First Sample Grammar, we will notice that there are two different results for the expression 2+4*2. The difference came from which operator we evaluated first. In the first tree, we can see that the multiplication sign was deeper in the tree. So we must evaluate it before evaluationg the addition, this gives the multiplication higer precedence than addition. In the other parse tree, the addition was deepre than the multiplication, and in this cas, we gave addition higer precedence than multiplication. So, to remove the ambiguity for that grammar, we need to ensure the correct precedence rule for arithmatic operations. In other words, we need to make sure that we always evaluate the multiplication first.
This problem illustrates how grammatical structure influences the evaluation of arithmetic expressions, and thus the semantics of programs. Note that, to get credit for this problem, you must solve it correctly three times in a row because the question is randomized. After you get the question right one time, the Check Answer button will then allow you to proceed to the next instance of the question.
Now let us try to remove the ambiguity for the grammar First Sample Grammar.
Example 12
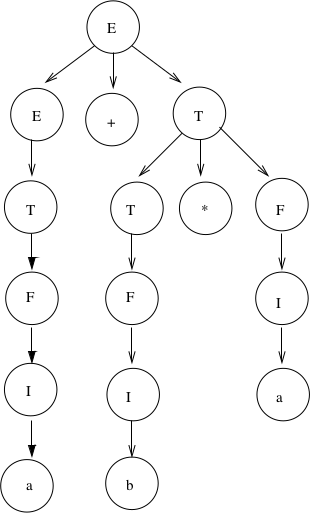
Rewrite the grammar as an unambiguous grammar. (Specifically, with the meaning that multiplication has higher precedence than addition.)
\(E \rightarrow E+T\ |\ T\)\(T \rightarrow T*F\ |\ F\)\(F \rightarrow I\ |\ (E)\)\(I \rightarrow a\ |\ b\)
There is only one derivation tree for \(a+b*a\):
Try to get a derivation tree with the other meaning of \(a+b*c\), when \(*\) is closer to the root of the tree.
\(E \Rightarrow T \Rightarrow T*F ...\) Then the only way to include a “\(+\)” before the multiplication is if the addition is enclosed in parenthesis. Thus, there is only one meaning that is accepted.
Let us see how the previous parse tree was built.
3.2. Associativity¶
3.3. Precedence and Associativity¶
This problem illustrates how grammatical structure impacts the associativity property and order of precedence of arithmetic operators.
Backus-Naur Form of a grammar:
Nonterminals are enclosed in brackets \(<>\)For “\(\rightarrow\)” use instead “\(::=\)”
Sample C++ Program::
main () {
int a; int b; int sum;
a = 40; b = 6; sum = a + b;
cout << "sum is "<< sum << endl;
}
“Attempt” to write a CFG for C++ in BNF (Note: \(<\mbox{program}>\) is start symbol of grammar.)
etc., Must expand all nonterminals!
So a derivation of the program test would look like:
This problem asks you to provide a characterization in English of the language generated by a BNF grammar. After you finish it, there is one more problem about Extended Backus-Naur Form, which is described before the problem.
4. Extended BNF¶
The symbols we have used in our representation of grammars collectively comprise what is known as Backus-Naur Form (BNF). In Extended Backus-Naur Form (EBNF) we add five meta-symbols to those already used in BNF notation:
Kleene closure operator \(*\), which means “zero or more”. Hence if \(<fn\_name>\) were a non-terminal representing a valid function name and \(<argument>\) were a non-terminal representing a valid argument, then the EBNF notation for function calls with zero or more arguments (with no commas between them) would be
\[<fn\_name> "(" <argument>* ")"\]Positive closure operator \(+\). The EBNF notation for function calls that must have at least one argument would be
\[<fn\_name> "(" <argument>+ ")"\]The two paired parenthesis symbols \(( \; )\), which are used for grouping. For example, if \(<positive\_number>\) were the non-terminal denoting a valid positive number, then the following EBNF would dictate that we must have a plus or minus sign preceding a number
\[(+ | -) <positive\_number>\]
The “optional operator” \(?\), which specifies that you can have zero or one of whatever grammatical structure precedes the operator. For example, if our language allowed an optional plus or minus sign in front of a number, we would use the EBNF
\[(+ | -)? <positive\_number>\]
EBNF is used to reduce the number of productions a grammar needs to specify a language. However, it does not increase the expressive power of grammars, that is, any grammatical structure that can be expressed in EBNF can also be expressed in BNF if one is willing to use more productions.
This last problem is about the equivalence between a given BNF grammar (the same one as in part 4 above) and a smaller EBNF grammar.
More on CFG for C++
Last time we “attempted” to write a CFG for C++, it is possible to write a CFG that recognizes all syntactically correct C++ programs, but there is a problem that the CFG also accepts incorrect programs. For example, it can’t recognize that it is an error to declare the same variable twice, once as an integer and once as a char.
We can write a CFG \(G\) such that \(L(G) = \{ \mbox{syntactically correct C++ programs} \}\).
But note that \(\{ \mbox{semantically correct C++ programs} \} \subset L(G)\).
Another example: Can’t recognize if formal parameters match actual parameters in number and type:
declare: int Sum(int a, int b, int c) …call: newsum = Sum(x,y);