1. Dimensions in an Array¶

So far when working with arrays, we’ve worked with one-dimensional arrays where we use a single subscript value to identify a position. You can imagine a one-dimensional array as a “line” of values.

However, sometimes you would like to represent data that is easier to think of as being arranged in a grid or a table instead of just a straight line. Java supports creating arrays with more than one subscript–which translates to more than one dimension.

A two-dimensional array is useful for certain kinds of problems. We often think of a two-dimensional array as being a rectangular grid, and use two subscript values instead of one. In fact, it turns out that if we imagine each individual “row” in the grid is its own one-dimensional array, then a rectangular grid is actually a series of rows arranged in a line–an array whose components are themselves arrays.

For example, you might use a two-dimensional of array (or 2D array, for short) if you are doing a scientific study in which you have to track the amount of precipitation for every day of the year, and you wanted to organize the day both by month and day. One way to organize these data would be to create a one-dimensional array, consisting of 365 elements:

double[] rainfall  = new double [ 365 ];

However, with this representation, it would make it very difficult to calculate the average rainfall within a given month, which might be an important part of your study.

A better representation for this problem would be to use a two-dimensional array, with one dimension for the months and one for the days.

The following statement declares the array variable rainfall and initializes it to refer to a newly created 12 by 31 array of double values:

double[] rainfall  = new double[12][31];

Thus, rainfall is an array of arrays. You can think of the first array as the 12 months required for the problem. And you can think of each month as an array of 31 days. The months will be indexed from 0 to 11, and the days will be indexed from 0 to 30.

The problem with this representation is that when we want to refer to the rainfall for January 5, we would have to use rainfall[0][4]. This is awkward and misleading, since we’d normally write the date as “1/5” if we were communicating with another person. The problem is that dates (like 12/31/2021) start their counting at 1, while arrays start counting at 0.

Because it will be difficult to remember this fact, our representation of the rainfall data may cause us to make errors when we start writing our algorithms. We can easily remedy this problem by just defining our array to have an extra month and an extra day each month:

double[] rainfall  = new double[13][32];

This representation creates an array with 13 months, indexed from 0 to 12, with 32 days per month, indexed from 0 to 31. However, we can simply ignore the 0 month and 0 day by using unit indexing (indexing starting with 1) in all of the algorithms that process the array. In other words, if we view this array as a two-dimensional table, consisting of 13 rows and 32 columns, we can leave row 0 and column 0 unused.

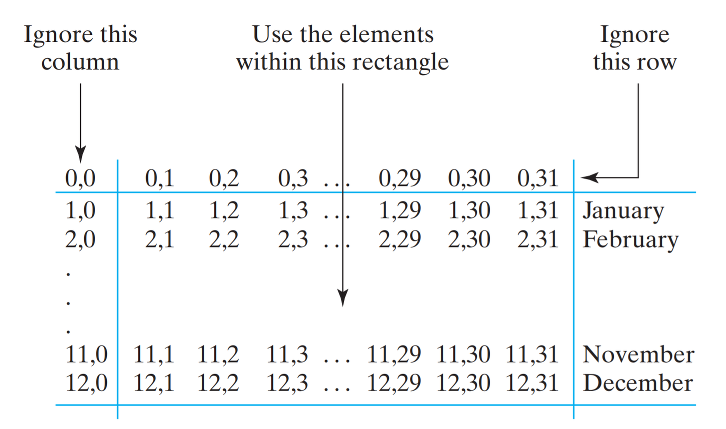
As the figure above shows, the very first element of this 416-element array has subscripts (0,0) while the last location has subscripts (12,31). The main advantages of this representation is that the program as a whole will be much easier to read and understand and much less prone to error.

In order to refer to an element in a two-dimensional array, you need to use two subscripts. For the rainfall array, the first subscript will specify the month and the second will specify the day within the month. Thus, the following statements assign 1.15 to the rainfall element representing January 5, and then print its value:

double[] rainfall  = new double[13][32];
rainfall[1][5] = 1.15; // rainfall for January 1st is 1.15

Just as in the case of one-dimensional arrays, it is an error to attempt to reference an element that is not in the array. Each of the following examples would cause an IndexOutOfBoundsException when executed:

double[] rainfall  = new double[13][32];
rainfall[13][32] = 1.15; // no such element
rainfall[11][33] = 1.15; // no such column
rainfall[14][2] = 1.15;  // no such row

2. Check Your Understanding: 2D Arrays¶

3. Syntax Practice: 2D Array Basics¶

4. Iterating through a 2D Array¶

As we’ve mentioned before, a double array will automatically initialize every value to 0.0 so we do not need to initialize the elements unless we want them to start with a different value. Remember if we were working with Strings or objects, this would not be the case!

However, for many array problems it is necessary to initialize the array elements to some other value. For a two-dimensional array, this would require a nested loop. To illustrate this algorithm, let’s use a nested pair of for loops to initialize each element of the rainfall array to 0:

for (int month = 1; month < rainfall.length ; month++)
{
    for (int day = 1 ; day < rainfall[month].length ; day++)
    {
        rainfall[month][day] = 0.0;
    }
}

Note that both for loops start at 1 since we’re not using row 0 or column 0.

Remember that when you have a nested for loop, the inner loop iterates faster. Thus, for each month, the inner loop will iterate over 31 days. This is equivalent to processing the array as if you were going across each row and then down to the next row in the representation shown in the picture in the previous section.

Note that for a two-dimensional array, both dimensions have an associated length, which is used in this example to specify the upper bound of each for loop. For the rainfall array, the first dimension (months) has a length of 13 and the second dimension (days) has a length of 32.

Another way to view the rainfall array is to remember that it is an array of arrays. The length of the first array, which corresponds to the number of months (13), is given by rainfall.length. The length of each month’s array, which corresponds to the number of days (32) in a month, is given by rainfall[month].length.

The outer loop of the nested for loop iterates through months 1 through 12, and the inner for loop iterates through days 1 through 31. In this way, 372 = 12 × 31 elements of the array are set to 0.0.

5. Check Your Understanding: Iterating with 2D Arrays¶

6. Syntax Practice: Looping Over 2D Arrays¶

7. Multi-Dimensional Arrays¶

Java doesn’t limit arrays to just two dimensions. For example, suppose we decide to extend our rainfall survey to cover a ten-year period. For each year we now need a two-dimensional array of months and days. This results in a three-dimensional array consisting of an array of years, each of which contains an array of months, each of which contains an array of days:

int years = 10;
int months = 13;
int days = 32;

double [][][] rainfall = new double[years][months][days];

Following the design convention of not using the 0 month and 0 days, we end up with a 10 × 13 × 32 array.

In the figure below, each year of the rainfall data is represented as a separate “page””. On each page, there is a two-dimensional table that consists of 12 rows (1 per month) and 31 columns (1 per day).

the following algorithm would be used to initialize all elements of our three-dimensional rainfall array:

for (int year = 0; year < rainfall.length ; year++)
{
    for (int month = 1 ; month < rainfall[year].length ; month++)
    {
        for(int day = 1 ; day < rainfall[year][month].length; day++)
        {
            rainfall[year][month][day] = 0.0;
        }
    }
}

Note again the proper use of the length attribute for each of the three dimensions of the array. In the outer loop, rainfall.length, we’re referring to the number of years. In the middle loop, rainfall[year].length, we’re referring to number of months within a given year. In the inner loop, rainfall[year][month].length, we’re referring to the number of days within a month.

If we added a fourth dimension to our array, to represent different ciites, for example, and wanted to extend this algorithm to initialize it, we would simply embed the three-level loop within another for loop that would iterate over each city.

int[] numbers = {1, 2, 3};

int[][] grid = {
    // two rows of 3 columns each
    {1, 2, 3},
    {4, 5, 6}
};
String[][][] arr3D = {
    // a 2x2x2 "cube" of strings
    {
        {"a", "b"},
        {"c", "d"}
    },
    {
        {"e", "f"},
        {"g", "h"}
    }
};

double[][] arrDifferent = {
    {1.0, 2.0, 3.0},
    {4.0, 5.0},
    {6.0, 7.0, 8.0, 9.0}
};

8. Syntax Practice: 3D Arrays¶

9. But Can You Have Multi-dimensional Lists?¶

One of the advantages that arrays provide over lists is that they have built-in support for stacking as many dimensions as necessary. Lists, on the other hand, have only a single dimension and a single integer position value you can use in their get() method.

Or do they? It turns out that just as a multi-dimensional array in Java can be thought of as an “array of arrays”, you can use the same concept to create a “list of lists” if you need a multi-dimensional list. After all, a list can contain any type of object, and lists themselves are objects, so it makes sense that you can put lists inside lists.

10. Integer Division and Modulus¶

Suppose you have a measurement in inches and you want to convert to feet and inches. The goal is divide by 12 (the number of inches in a foot) and keep the remainder.

We have already seen the division operator (/), which computes the quotient of two numbers. If the numbers are integers, it performs integer division, which throws away any fractional part of the answer, discarding any remainder.

Java also provides the modulus operator (%), which divides two numbers and computes the remainder.

Using division and modulus, we can convert to feet and inches like this:

int quotient = 76 / 12;  // division
int remainder = 76 % 12; // modulus

The first line yields 6. The second line, which is pronounced “76 mod 12”, yields 4. So 76 inches is 6 feet, 4 inches.

The modulus operator looks like a percent sign, but you might find it helpful to think of it as a division sign (÷) rotated to the left.

The modulus operator turns out to be surprisingly useful. For example, you can check whether one number is divisible by another: if x % y is zero, then x is evenly divisible by y with no remainder.

For example, if we wanted to write an if statement that only ran if an int x was divisible by 5, we’d write:

if (x % 5 == 0)
{
    // do some action
}

You also can use modulus to “extract” digits from a number: x % 10 yields the rightmost digit of x, which is the same as the remainder after dividing x by 10. Similarly, x % 100 yields the last two digits. You can combine this with division, since x / 10 is the digits without the rightmost digit. For example, the number 1234 consists of 123 (which is x / 10) followed by 4 (which is x % 10).

Also, many encryption algorithms use the modulus operator extensively.

Here are two really short videos you can check out that will help explain modulo arithmetic as well:

11. Check Your Understanding: Modulus¶

12. Syntax Practice: Modulus¶

13. Programming Practice: Multi-dimensional Arrays¶

14. Programming Practice: Mod¶