LR Parsing¶

1. LR Parsing¶

1.1. LR(k) Parser¶

The LL(k) parser was simple, but not much power. It can’t recognize a lot of languages.

LR(k) is more powerful but also more complicated!

Is a shift-reduce parser: shifts terminals onto a stack until the right-hand-side of a rewrite rule can be reduced to the left-hand-side of its rule.
Is a bottom-up parser: Starts with input string, repeatedly replaces right-hand-side of rewrite rules with left-hand-side until we reach the start symbol. (So this is the opposite of the LL parser, which went “top down” from the start symbol to the string.)
L means: reads input left to right
R means: produces a rightmost derivation (LL was a leftmost derivation)
$k$: number of lookahead symbols

Note

We will just examine LR(1) grammars

Remember that LL(1) parsing routine was constructed by converting a CFG to a PDA.

1.2. LR parsing process¶

Convert CFG to PDA (uses a different conversion process than the LL process)
Use the PDA and lookahead symbols (Uses a different parsing routine than LL process)

Convert CFG to PDA

Idea: To derive a string from a CFG with a rightmost derivation, start with the start symbol and repeatedly apply productions replacing the rightmost variable at each step. In order to simulate this process with an NPDA, we will simulate this process in reverse by starting with the input string, using productions in reverse (replacing right-hand-side of a production by its left-hand-side), and deriving the start symbol. Thus, the NPDA starts by shifting the symbols of the input string onto the stack. Whenever the top symbols on the stack match the right-hand-side of a production, pop the right-hand-side (may be several symbols) and replace it (or push) the left-hand-side on the stack. If replacements lead to only the start symbol on the stack, then the input string is in the language of the grammar. To see the actual rightmost derivation the NPDA simulated, start with the start symbol and apply the productions in the reverse order they were applied in the NPDA.

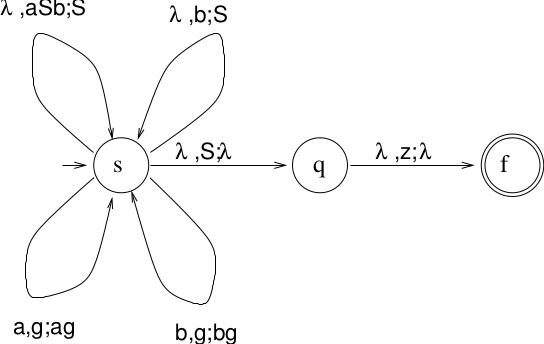
The constructed NPDA:

Three states: $s, q, f$

Start in state $s$, put bottom marker $z$ onto stack
All rewrite rules in state $s$, backwards

Rules pop right-hand-side, then push left-hand-side

$(s, \mbox{lhs}) \in \delta(s, \lambda, \mbox{rhs})$

Note: We assume that the stack can pop several symbols at once.

This is called a reduce operation.
Additional rules in $s$ to recognize terminals

For each $x \in \Sigma, g \in \Gamma, (s,xg) \in \delta(s,x,g)$

This is called a shift operation.
Pop $S$ from stack and move into state $q$
Pop $z$ from stack, move into $f$, accept.

Example 1

Construct a PDA.

$L = \{a^nbb^n: n \ge 0\}$

$S \rightarrow aSb$

$S \rightarrow b$

(where there is an arc for each $g \in \Gamma$).

Note

Trace string $aabbb$

PDA is nondeterministic! Use the lookahead to decide which transition to apply.

1.3. LR Parsing Actions¶

Shift

Transfer the lookahead to the stack
Reduce

For $X \rightarrow w$, replace $w$ by $X$ on the stack
Accept

Input string is in language
Error

Input string is not in language

We want to save all this information in a table.

1.4. LR(1) Parse Table¶

Columns:

Terminals, $\$$ and variables ($\$$ is end-of-string marker)

Terminals and $\$$ are used lookaheads.

Variables are sortof used as a lookahead.
Rows:

State numbers: represent patterns in a derivation

LR(1) Parse Table Example

1) $S \rightarrow aSb$

2) $S \rightarrow b$

\[\begin{split}\begin{array}{|r||c|c|c|c|} \hline &a & b & \$ & S \\ \hline \hline 0 & s2 & s3 & & 1 \\ \hline 1 & & &acc & \\ \hline 2&s2&s3&&4 \\ \hline 3&&r2&r2& \\ \hline 4&&s5&& \\ \hline 5&&r1&r1& \\ \hline \end{array}\end{split}\]

Definition of entries:

$sN$: Shift (or push) the terminal for this column onto the stack, and move to state (or row number) N.
$N$: Move to state (or row number) N.
$rN$: Reduce by rule number N. The rhs of this rule is on the top of the stack. Pop it and replace it by the lhs of the rule.
$acc$: The input string is accepted.
Blank: Error.

Note

Identify each type of operation

We will create a DFA that models the stack contents. When there is a rhs on top of the stack, we reduce, we are in a final state.

The state numbers on the stack are just a trace of where we came from.

LR(1) Parsing routine

“entry” is a record with four parts: state, action, rule.rhs, rule.lhs:

state = 0
push(state)
read(symbol)                                 obtain the lookahead symbol
entry = T[state,symbol]                      T is the LR parse table
while entry.action <> accept do
   if entry.action == shift then
      push(symbol)
      state = entry.state
      push(state)
      read(symbol)
   else if entry.action == reduce then
      do 2*size_rhs times { pop() }         pop entry.rule.rhs and states
      state := top-of-stack()               do not pop!
      push(entry.rule.lhs)
      state = T[state,entry.rule.lhs]
      push(state)
   else if entry.action == blank then
      error
   entry = T[state, symbol]
end while
if symbol <> $ then error

Example 2

Trace $aabbb$

\[\begin{split}\begin{array}{rcccccccccc} & & & & & &5 \\ & & & & & &b \\ & & & & 3 &4 &4 &&5 \\ & & & & b &S &S &&b \\ & & & 2 &2 &2 &2 &4 &4 \\ & & & a &a &a &a &S &S \\ & & 2 & 2 &2 &2 &2 &2 &2 &1 \\ & & a & a &a &a &a &a &a &S \\ & 0 & 0 & 0 &0 &0 &0 &0 &0 &0 \\ \mbox{Stack:} &\underline{z} &\underline{z} &\underline{z} & \underline{z} &\underline{z} &\underline{z} &\underline{z} &\underline{z} & \underline{z} \\ \mbox{Lookahead:} & a & a & b & b &b &b &b &\$ & \$ \\ \mbox{Action:} & sh & sh & sh &red &sh &red &sh &red & acc \\ \end{array}\end{split}\]

Note

Fill in actions.

To construct the LR(1) parse table: (idea)

Construct a DFA (transition diagram) to model the top of the stack whose states represent the current contents of the parsing stack.

Note: DFA!
Using the DFA, construct an LR(1) parse table

To Construct the DFA

Idea: The states in the DFA will contain marked productions that indicate what is currently on the top of the stack, and what additional symbols need to be pushed onto the stack in order for a rhs to be on top of the stack, so a reduce operation can occur.

Add a new production $S' \rightarrow S$ to the grammar, where $S'$ is the new start symbol.

Note: This is done so that when the start symbol is on the stack, that means the string is accepted. That would not be the case if the start symbol is used on some rhs.
Place a marker “_” on the rhs of the production to indicate status of parsing process.

$S' \rightarrow \_S$

The items in the rhs to the left of the marker are the items we have parsed (they are on the top of the stack), and the items to the right of the marker are the items we have not seen yet (still need to be pushed onto the stack).

Example: $A \rightarrow a\ {\_}\ Ab$ indicates that “a” is on top of the stack and we need to push “A” and “b” on the stack before we can reduce “aAb” to “A”.
Compute the set of productions $\mbox{closure}(S' \rightarrow \_S)$.

Definition of closure:
1. $\mbox{closure}(A \rightarrow v\_xy) = \{A \rightarrow v\_xy\}$ if $x$ is a terminal.
2. $\mbox{closure}(A \rightarrow v\_xy) = \{A \rightarrow v\_xy\} \cup (\mbox{closure}(x \rightarrow \_w)$ for all $w$ (where $w$ is the right hand side of a production in which $x$ is the left hand side)) if $x$ is a variable.
NOTE: This is a recursive definition.
The $\mbox{closure}(S' \rightarrow \_S)$ is designated as state 0 and marked as “unprocessed”.
Repeat until all states have been processed
- unproc = any unprocessed state
- For each $x$ that appears in $A \rightarrow u\_xv$ (where the A production is from the state “unproc”) do
  - Add a transition labeled “x” from state “unproc” to a new state with production $A \rightarrow ux\_v$
    
    (Note: If there is more than one production in state “unproc” that has a marker before the $x$, then one new state is created and all of these productions are placed into the new state, with the marker moved to the right of the $x$)
  - The set of productions for the new state are: $\mbox{closure}(A \rightarrow ux\_v)$
    
    (Note: If there was more than one production put in from the previous step, then closure is applied to all of those productions).
  - If the new state is identical (has same productions and marker positions) to another state, then combine the two states into one state. Otherwise, mark the new state as “unprocessed”
Identify final states. Any state that has at least one production with “_” at the end of the rhs is a final state.

Example 3

Construct DFA

$S' \rightarrow S$
$S \rightarrow aSb$
$S \rightarrow b$

Backtracking through the DFA

Short Version:

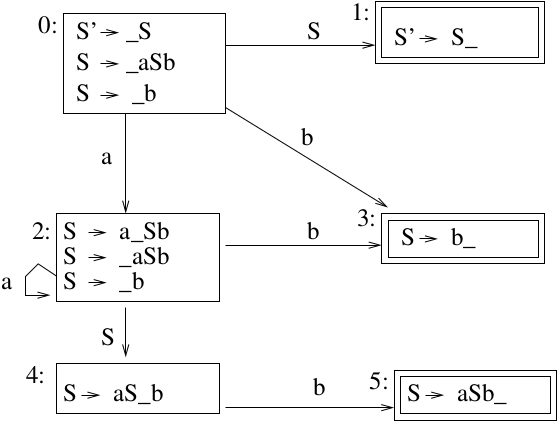
Consider $aabbb$

Start in state 0.
Shift “a” and move to state 2.
Shift “a” and move to state 2.
Shift “b” and move to state 3.

Reduce by “$S \rightarrow b$”

Pop “b” and Backtrack to state 2.

Shift “S” and move to state 4.
Shift “b” and move to state 5.

Reduce by “$S \rightarrow aSb$”

Pop $aSb$ and Backtrack to state 2.

Shift “S” and move to state 4.
Shift “b” and move to state 5.

Reduce by “$S \rightarrow aSb$”

Pop “aSb” and Backtrack to state 0.

Shift “S” and move to state 1.
Accept. $aabbb$ is in the language.

A More detailed explanation of the Backtracking

A state in the DFA represents what is currently on “top” of the stack. A state is a final state if it represents the fact that a right hand side is on top of the stack.

Consider the string $aabbb$. We will trace the string through the DFA.

Start in state 0, the start state. We have not recognized any part of the string yet.

We recognize the first “a” in the string (shift the “a” onto the stack) and move into state 2. State 2 represents the fact that “$aa^*$” is on top of the stack. In this case, “a” is on top of the stack.

We recognize the second “a” in the string (shift it onto the stack) and remain in state 2. The stack now contains “aa” which is in the form $aa^*$.

We recognize the first “b”, shift it onto the stack, and move into State 3. State 3 represents the fact that $aa^*b$ or $b$ is on top of the stack. In this case, $aab$ is on the stack (with “b” on top). We now have the right hand side of a production rule on top of the stack. This is why State 3 is a final state. Final states indicate that a reduction is possible. We apply the reduction $S \rightarrow b$. We will pop “b” from the stack and backtrack in the DFA back to state 2, since the current contents on the stack is now $aa$ (which state 2 represents). We will push “math:S onto the stack and move from state 2 to state 4, since state 4 represents $aa^*S$, and $aaS$ is now the contents of the stack.

We recognize the second “b” in the string, shift it onto the stack and move into state 5, which represents that the current stack contents are in the form $aa^*Sb$, in this case they are $aaSb$. State 5 is a final state, which means that the right hand side of the production “$S \rightarrow aSb$” is on top of the stack. We can reduce by this production. We will pop $aSb$ from the stack, and backtrack in the DFA from state 5 to state 4 to state 2 to state 2. The current contents of the stack is now “a”, which is represented by state 2. We push $S$ onto the stack and move into state 4. The current stack contents are $aS$.

We recognize the third “b” in the string, shift it onto the stack and move into state 5. Current stack is $aSb$. We reduce, popping $aSb$ from the stack and backtrack from State 5 to State 4 to state 2 to state 0. The current contents of the stack are empty. We push $S$ onto the stack and move into State 1, which represents that the stack contents are $S$, our goal. The string is accepted.

Note the productions identified in order are:

\(S \rightarrow b\)
\(S \rightarrow aSb\)
\(S \rightarrow aSb\)
\(S' \rightarrow S\)

In reverse order the productions and the corresponding derivation is:

\[\begin{split}\begin{array}{lll} S' \rightarrow S & \ \ \ \ \ \ \ \ \ \ \ \ & S' \Rightarrow S\\ S \rightarrow aSb && \Rightarrow aSb \\ S \rightarrow aSb && \Rightarrow aaSbb \\ S \rightarrow b && \Rightarrow aabbb \\ \end{array}\end{split}\]

To construct LR(1) table from diagram:

If there is an arc from state1 to state2
1. Arc labeled $x$ is terminal or $
  
  T[state1, x] = state2
2. Arc labeled $X$ is nonterminal
  
  T[state1, X] = state2
If state1 is a final state with $X \rightarrow w\_$

For all $a$ in $\mbox{FOLLOW}(X)$, T[state1, a] = reduce by $X \rightarrow w$

(or T[state1, a] = rN where N is the number of the production $X \rightarrow w$)
If state1 is a final state with $S' \rightarrow S\_$

T[state1, $] = accept
All other entries are error

Example: LR(1) Parse Table

(0) $S' \rightarrow S$

(1) $S \rightarrow aSb$

(2) $S \rightarrow b$

Here is the LR(1) Parse Table with extra information about the stack contents of each state.

\[\begin{split}\begin{array}{|r|r||c|c|c|c|} \hline \mbox{Stack} & \mbox{State} & \multicolumn{3}{c}{\mbox{Terminals}} & \mbox{Variables} \\ \cline{3-6} \mbox{contents}&\mbox{number}&a & b & \$ & S \\ \hline\hline \mbox{(empty)}&0 & s2 & s3 & & 1 \\ \hline S&1 & & &acc & \\ \hline aa^*&2&s2&s3&&4 \\ \hline aa^*b \mid b&3&&r2&r2& \\ \hline aa^* S&4&&s5&& \\ \hline aa^* Sb&5&&r1&r1& \\ \hline \end{array}\end{split}\]

Actions for entries in LR(1) Parse table T[state,symbol]

Let entry = T[state,symbol].

If symbol is a terminal or $
- If entry is “shift $\mbox{state}i$”
  
  Push lookahead and $\mbox{state}i$ on the stack
- If entry is “reduce by rule $X \rightarrow w$”
  
  Pop $w$ and $k$ states ($k$ is the size of $w$) from the stack. Let $\mbox{state}i$ be the state currently on top of the stack. Push $X$ onto the stack. Push $\mbox{state}j$ onto the stack, where $\mbox{state}j =$ T[statei, X].
- If entry is “accept”
  
  Halt. The string is in the language.
- If entry is “error”
  
  Halt. The string is not in the language.
If symbol is nonterminal

We have just reduced the rhs of a production $X \rightarrow w$ to a symbol. The entry is a state number, call it $\mbox{state}i$. Push T[statei, X] onto the stack.

Constructing Parse Tables for CFG’s with $\lambda$ rules

$A \rightarrow \lambda$ written as $A \rightarrow \lambda\_$

A $\lambda$-rule is recognized as being reducible right away. Any state that has a $\lambda$-rule is a final state that can apply the $\lambda$-rule as a reduction.

It doesn’t make sense to push $\lambda$ onto the stack, so there won’t be any arcs with $\lambda$. (Besides, allowing $\lambda$ in our DFA would turn our DFA into an NFA!). For the rule “$A \rightarrow \lambda$”, we enter it into the table for any lookahead that is in $\mbox{FOLLOW}(A)$.

Example 4

\(S \rightarrow ddX\)
\(X \rightarrow aX\)
\(X \rightarrow \lambda\)

Add a new start symbol and number the rules:

(0) \(S' \rightarrow S\)
(1) \(S \rightarrow ddX\)
(2) \(X \rightarrow aX\)
(3) \(X \rightarrow \lambda\)

Construct the DFA:

Construct the LR(1) Parse Table

NOTE: $\mbox{FOLLOW}(S) = \mbox{FOLLOW}(X) = \{\$\}$

\[\begin{split}\begin{array}{|l||l|l|l|l|l|} \hline & a & d & \$ & S & X \\ \hline \hline 0 & & s 2 & & 1 & \\ \hline 1 & & & acc & & \\ \hline 2 & & s 3 & & & \\ \hline 3 & s 5 & & r 3 & & 4 \\ \hline 4 & & & r 1 && \\ \hline 5 & s 5 & & r 3 & & 6 \\ \hline 6 & & & r 2 & & \\ \hline \end{array}\end{split}\]

Note: For another example of constructing an LR(1) Parse Table, see the project 3 handout.

Conflicts when constructing an LR Parse Table

If you try to construct an LR(1) Parse Table and there are two items in an entry in the table, then the grammar is not LR(1).

Possible Conflicts:

Shift/Reduce Conflict - The right hand side of a production rule is on top of the stack. It is also possible to shift more symbols and have another rhs on top of the stack.

Example: Suppose a grammar contains the following 2 production rules:

$A \rightarrow ab$

$A \rightarrow abcd$

Note

Add rule $S \rightarrow bAc$, then $c \in \mbox{FOLLOW}(A)$.

Then there will be a state in the DFA that will contain

$A \rightarrow ab\_$

$A \rightarrow ab\_\ cd$

The first rule indicates a REDUCE (thus this state will be a final state). The second rule indicates a SHIFT. If you shift c and then d onto the stack, then you can reduce by the second rule.

So, do you reduce by “ab” or shift the “c”? Conflict!
Reduce/Reduce Conflict

There is a state that contains two rules with identical right hand sides.

Example: Suppose a grammar contains the following two production rules:

$A \rightarrow ab$

$B \rightarrow ab$

Then there could be a state in the DFA that will contain

$A \rightarrow ab\_$

$B \rightarrow ab\_$

You know that you want to replace ab, but you don’t know which rule to apply. Conflict!
Shift/Shift Conflict

This cannot happen since the diagram is a DFA. There is a unique state to move into for each symbol.

OpenDSA Stand-alone Modules

Chapter 0 modules

LR Parsing¶

1. LR Parsing¶

1.1. LR(k) Parser¶

1.2. LR parsing process¶

1.3. LR Parsing Actions¶

1.4. LR(1) Parse Table¶