Regular Grammars¶
1. Regular Grammars¶
Here is another way to describe a regular language.
Grammar \(G = (V, T, S, P)\)
\(V\), \(T\), and \(P\) are finite sets.
Right-linear grammar:
Note: \(x\) is a string of length 0 or more.
Left-linear grammar:
Definition:
A regular grammar is a right-linear or left-linear grammar.
Note
There is a more restrictive definition in which the length of \(x\) is \(\leq 1\). (Exercise in book.)
Example 1
The language is \((ab)*\).
However, cannot mix left/right rules! So this is not a regular grammar.
Example 2
This is a right linear grammar representing the language \(L = \{ \mbox{strings with an even number of a's}\}, \Sigma = \{a,b\}\)
1.1. Our Next Step¶
1.2. NFA from Regular Grammar¶
Theorem: L is a regular language if and only if \(\exists\) regular grammar G such that \(L = L(G)\).
(Doing here for RR grammar, see book for proof sketch for LR grammar.)(\(\Longleftarrow\)) Given a regular grammar G, Construct NFA M such that \(L(G)=L(M)\)Make a state for each non-terminal.Make a transition on each terminal in that production rule.Make it final if there is a production without non-terminals.For rules with multiple terminals, need intermediate states.
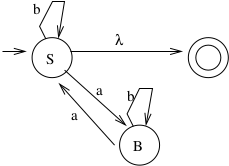
Example 3
What about a rule like \(S \rightarrow abB\)? Make two states (S to intermediate state on a, then intermediate state to B on b).
Or \(S \rightarrow ab\)? Make two states (S to intermediate state on a, then intermediate state to an accepting state on B.
1.3. Right-linear Regular Grammar from DFA¶
Theorem: L is a regular language iff \(\exists\) regular grammar G such that \(L = L(G)\).
(\(\Longrightarrow\)) Given a DFA \(M\), construct regular grammar \(G\) such that \(L(G)=L(M)\)
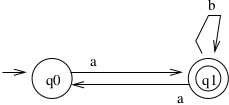
The process is pretty much the same as when we made an NFA from RRG:Each DFA state gets a non-terminal.Each transition gets a production rule.Construct the Regular Grammar for the NFA
\(G = (\{S,B\},\{a,b\},S,P)\),\(P =\)\(Q0 \rightarrow a Q1\)\(Q1 \rightarrow a Q0 | b Q1 | \lambda\)
1.4. Something to Think About¶
Example 4
\(L = \{a^nb^n \mid n>0\}\)
Is language \(L\) regular? Can you draw a DFA, regular expression, or Regular grammar for this language?
Consider this grammar:
\(S \rightarrow aSb \mid ab\)
Nice and easy... but this grammar is not regular!
We will come back to this question later.