Minimizing the Number of States in a DFA¶
1. Minimizing the Number of States in a DFA¶
Why do we need to do this?
If you have an NFA with \(n\) states, what is the maximum number of states in the equivalent DFA created? \(2^n\)
Algorithm
Identify states that are indistinguishable
- These states form a new state in the minimized machine.
Definition: Two states \(p\) and \(q\) are indistinquishable if for all \(w \in \Sigma^*\)
Definition: Two states \(p\) and \(q\) are distinquishable if \(\exists\ w \in \Sigma^*\) such that
All that an acceptor cares about is accepting or rejecting strings.
Select any pair of states, \(p\) and \(q\).
- If, in either case, we accept/reject the exact same set set of strings, then there is no difference between them.
- So, we can combine them.
Distinguishability is an equivalence relation. We are trying to break the set of all states into subsets that are equivances.
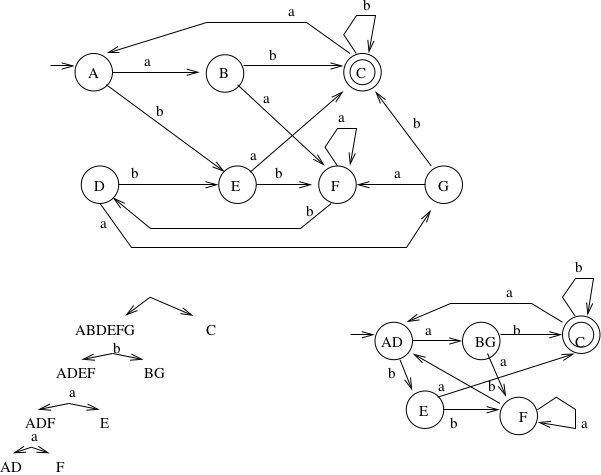
Example:
Look at A on \(a\), \(ab\):
- \(a\) goes to a non-final state, \(ab\) goes to a final state
Look at F on \(a\), \(ab\):
- \(a\) goes to a non-final state, \(ab\) goes to a non-final state
Look at D on \(a\), \(ab\):
- \(a\) goes to a non-final state, \(ab\) goes to a final state
So, we know that F must be in a different equivalence subset than A and D. A and D might or might not end up being equivalent, we don't have enough evidence yet to decide.
Unfortunately, this is not obviously an algorithm, since we cannot actually test on all input strings.
- But remember the definition for \(\delta^*(p, w)\). Look at things this way: It is telling us that we don't care about the prior history before we got to the current state with whatever remains of the input.
- So, we can look at each transition out of two subsets being considered, and verify that they lead to "equivalent" places (which is not the same as leading to the same state in the non-minimized machine).
- We will start with the maximum possible joining of states as a potential equivalence class, and see if we find evidence that forces us to break them apart as we consider the various transitions.
We will build a tree, whose root has all states in the original machine. The first step will always be to split the states into the subset of non-final vs. the subset of final states, so these are the children of the root. We then look at each current leaf node of the tree, and check the transitions from each of the states in that leaf. We test a given character against the states in that subset to see if they all go to the same subset. Split them up when they do not go to the same place.
The following slideshow presents, step-by-step, the process of minimizing the DFA.
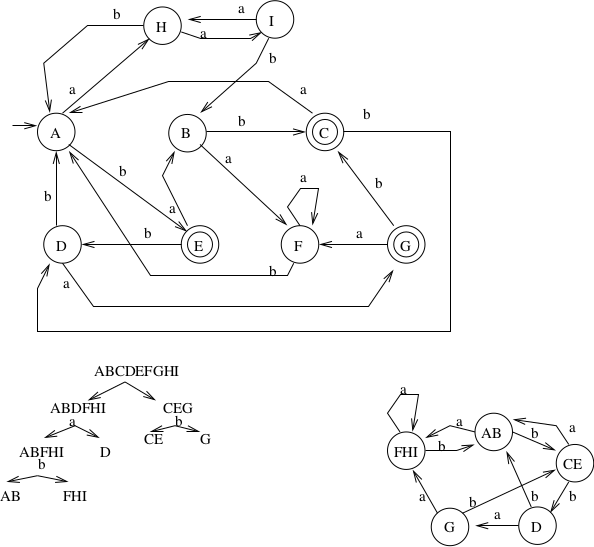
Another Example: