LL Parsing¶
1. LL Parsing¶
1.1. LL(k) Parser¶
Top-down parser: starts with start symbol on stack, and repeatedly replace nonterminals until string is generated.
- Predictive parser: predict next rewrite ruleNOTE: use lookahead for this
First L of LL means that we read input string left to right
Second L of LL means that we produce the leftmost derivation
Note
ASK TO SEE IF THEY KNOW WHAT THIS IS
- \(k\): number of lookahead symbols used.Sometimes more than one symbol is needed
1.2. LL parsing process¶
- Convert CFG to PDA (different method than before)
- Use the PDA and lookahead symbols
- Lookahead symbol is next symbol in input string
Notes:
- The PDA is nondeterministic, so we will lookahead to the next input symbol and use it to determine which rewrite rule to use.
- Nondeterministic, could use back-tracking, but this could take forever.
- Remember: cannot necessarily construct a deterministic PDA from a NPDA.
1.3. Convert CFG to NPDA¶
NOTE: This is not the same construction method we used before. This method will apply to any CFG, even those that are not in GNF.
Idea: To derive a string with a CFG, start with the start symbol and repeatedly apply production rules until the string is derived. In order to simulate this process with an NPDA, start by pushing the start symbol on the stack. Whenever a production rule \(A \rightarrow w\) would be applied, the variable \(A\) should be on top of the stack. \(A\) is popped (or replaced) and the right hand side of the rule, \(w\), is pushed onto the stack. Whenever a terminal is on top of the stack, if it matches the next symbol in the input string, then it is popped from the stack. If it does not match, then this string is not in the language of the grammar. If starting with the start symbol \(S\), one can apply replacement rules, match all the terminals in the input string and empty the stack, then the string is in the language.
Note
Just mention this stuff and then draw NPDA.
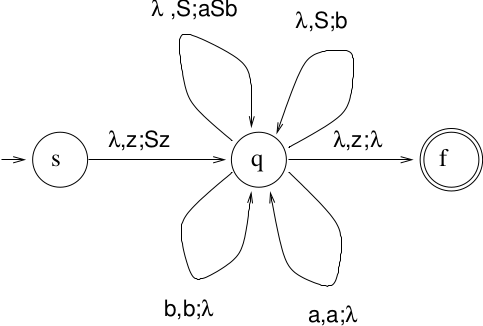
The constructed NPDA:
- Three states: \(s, q, f\)As usual, start in state \(s\)Push \(S\) on stack, move into \(q\)All rewrite rules in state \(q\): If left-hand-side of rewrite rule on top of stack, replace it with right-hand-side of rewrite rule and stay in state \(q\)Additional rules in \(q\) to recognize terminals: Read input symbol, pop input symbol, stay in state \(q\)Pop \(z\) from stack, move into \(f\), accept
Example 1
Note that this is nondeterministic. You have to use the lookahead to decide which transition to take, in a sense adding determinism by using extra information.
Note
Trace aabbb.
symbolis a buffer that holds next input symbol (not processed right away)- We have gotten rid of the nondeterminism by using the lookahead symbol.
A parsing routine for this grammar:
symbol is the lookahead symbol and $ is the end-of-string marker:
state = s
push(S)
state = q
read(symbol) obtain the lookahead symbol
while top-of-stack <> z do while stack is not empty
case top-of-stack of
S: if symbol == a then cases for variables
{ pop(); push(aSb) } replace S by aSb
else if symbol == b then
{ pop(); push(b) } replace S by b
else error
a: if symbol <> a, then error cases for terminals
else { pop(); read(symbol) } pop a, get next lookahead
b: if symbol <> b, then error
else { pop(); read(symbol) } pop b, get next lookahead
end case
end while
pop() pop z from the stack
if symbol <> $ then error
state = f
What are drawbacks?
- for larger grammar, case statement can get quite
Can put the case statement into a generic routine
1.4. LL Parse Table: 2-dimensional array¶
When the grammar is large, the parsing routine will have many cases. Alternatively, store the information for which rule to apply in a table.
- Rows: variables
- Columns: terminals, $ (end of string marker)
LL[i,j]contains the right-hand-side of a rule. This right-hand-side is pushed onto the stack when the left-hand-side of the rule is the variable representing the \(i\) th row and the lookahead is the symbol representing the \(j\) th column.- If we can specify any CFG by this type of parse table, then we can use a generic parser to determine if strings are in this language.
- Gets rid of use of states
Example 2
Parse table for
1.5. A generic parsing routine¶
Idea: To replace a variable on the top of the stack with
its appropriate right-hand-side, use the lookahead
and the left-hand-side to look up the right-hand-side in the LL parse
table.
(LL[,] is the parse table.):
push(S)
read(symbol) obtain the lookahead symbol
while stack not empty do
case top-of-stack of
terminal:
if top-of-stack == symbol
then { pop(); read(symbol) } pop terminal and get next lookahead
else
error
variable:
if LL[top-of-stack, symbol] <> error
then { pop(), pop the lhs
push(LL[top-of-stack,symbol]) } push the rhs
else
error
end case
end while
if symbol <> $, then error
Note
For previous example, try the following traces:
Parse the string: aabbb
Parse the string: b
Example 3
In this example, it is clear that when \(S\) is on the stack and \(a\) is the lookahead, replace \(S\) by \(aSb\). When \(S\) is on the stack and \(b\) is the lookahead, there is an error, because there must be a \(c\) between the \(a\) 's and \(b\) 's. When \(S\) is on the stack and $ is the lookahead, then there is an error, since \(S\) must be replaced by at least one terminal. When \(S\) is on the stack, and \(c\) is the lookahead, then \(S\) should be replaced by \(c\).
Example 4
When the grammar has a \(\lambda\)-rule, it can be difficult to compute parse tables. In this example, \(A\) can disappear (due to \(A \rightarrow \lambda\)), so when \(S\) is on the stack, it can be replaced by \(Ac\) if either "a" or "c" are the lookahead, or it can be replaced by \(Bc\) if "b" is the lookahead.
We will use the following functions FIRST and FOLLOW to aid in computing the table.
1.6. To construct an LL parse table LL[rows,cols]¶
Note
Refresh memory as to what parse table is.
For each rule \(A \rightarrow w\)
- For each a in FIRST(w)add w to LL[A,a]
- If \(\lambda\) is in FIRST(w)add \(w\) to LL[A,b] for each \(b\) in FOLLOW(A)where \(b \in T \cup \{\$\}\)
Each undefined entry is an error.
Example 5
We have already calculated FIRST and FOLLOW for this Grammar:
To Compute the LL Parse Table for this example:
- For \(S \rightarrow aSc\),\(\mbox{FIRST}(aSc) = \{a\}\), so add \(aSc\) to
LL[S,a]by step 1a. - For \(S \rightarrow B\),\(\mbox{FIRST}(B) = \{b, \lambda \}\)\(\mbox{FOLLOW}(S) = \{\$, c\}\)By step 1a, add \(B\) to
LL[S,b]By step 1b, add \(B\) toLL[S,c]andLL[S,$] - For \(B \rightarrow b\),\(\mbox{FIRST}(b) = \{b\}\), so by step 1a add \(b\) to
LL[B,b] - For \(B \rightarrow \lambda\)\(\mbox{FIRST}(\lambda) = \{ \lambda \}\) and \(\mbox{FOLLOW}(B) = \{\$, c\}\), so by step 1b add \(\lambda\) to
LL[B,c]and add \(\lambda\) toLL[B,$].
LL(1) Parse Table
Parse string: \(aacc\)
where \(a'\) is the second \(a\) in the string and symbol is
the lookahead symbol.
This table is an LL(1) table because only 1 symbol of lookahead is needed.
Example 6
Trace \(aabcc\)
where \(a'\) is the second \(a\) in the string and symbol
is the lookahead symbol.
This table is an LL(1) table because only 1 symbol of lookahead is needed.
Example 7
\(S \rightarrow AcB\)\(A \rightarrow aAb\)\(A \rightarrow \lambda\)\(B \rightarrow aBb\)\(B \rightarrow c\)
LL[S,a]andLL[S,c]LL[A,a]LL[A,b]andLL[A,c]LL[B,a]LL[B,c]
parse string: \(abcacb\)
parse string: \(cc\)
parse string: \(abcab\) (not in language)
Example 8
Note that FIRST and FOLLOW are quite easy to calculate since there are no \(\lambda\) rules! In this case, you don't need FOLLOW to construct the parse table.
Try to construct LL(1) Parse table
Note that you don`t know which rewrite rule to apply to replace
\(A\) and \(B\) with just one lookahead symbol.
\(A\) has two choices and both use a lookahead of 'a'.
There are two entries in the LL(1) parse table for T[A,a].
Thus, there is no LL(1) parse table.
This means the grammar is not LL(1)!.
We will try to use 2 symbols of lookahead.
For example, the string \(aabbcaacbb\) cannot be parsed with just one lookahead.
LL(2) Parse Table:
There are no conflicts (only one rule in each entry of the table). This is an LL(2) parser - need two lookahead symbols.
parse string: \(aabbcacb\)
Note the leftmost derivation! Also note that the two lookahead symbols are used whenever there is a variable on top of the stack.
An LL(k) parser needs \(k\) lookahead symbols.
Note
Mention that LL parser doesn't work if the grammar is left recursive.
Example 9
\(L = \{a^n: n \ge 0 \} \cup \{a^nb^n: n \ge 0 \}\)
\(S \rightarrow A\)\(S \rightarrow B\)\(A \rightarrow aA\)\(A \rightarrow \lambda\)\(B \rightarrow aBb\)\(B \rightarrow \lambda\)
This grammar cannot be recognized by an LL(k) parser for any \(k\)! Consider the string \(aabb\). You would need 3 lookahead to realize that you want to use \(S \rightarrow B\). Consider the string \(aaabbb\), you would need 4 lookahead. Consider string \(a^nb^n\), you would need \(n\) lookahead. There is no (constant) \(k\) such that \(k\) lookahead works for every string in the language.
Example 10
An LL(11) parser will work since all strings have 10 or fewer \(a\) 's.
Example 11
This grammar is LL(5). We don't know which S rule to apply with the string \(bbccd\) or \(bbcc\$\) until you have seen the fifth symbol.
This grammar cannot be recognized by an LL(k) parser.
When the lookahead is \(b\), don't know which rule to apply, either the second or third.
Comments:
There are some CFL's that have no LL(k) Parser
There are some languages for which some grammars have LL(k) parsers and some don't.