Recursively Enumerable Languages¶
1. Recursively Enumerable Languages¶
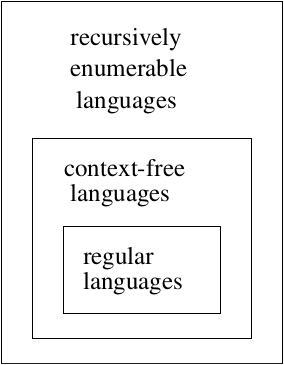
What is the set of languages that TM's accept? We know that they accept RL's and CFL's. And additional languages.
Question: Is there any language that a TM cannot accept?
Definition: A language \(L\) is recursively enumerable if there exists a TM \(M\) such that \(L = L(M)\).
[Hah! All that says is that the languages that a TM can deal with now have a name!]
We say that \(M\) accepts the language. For every \(w\) in \(L\), \(M\) should accept \(w\).
Question: What happens if \(w\) is not in \(L\)? Saying that \(M\) can properly accepting strings in \(L\) doesn't define happens if \(w\) is not in \(L\). \(M\) may not halt in that case.
Note: We do not get a yes or no answer, just a yes if w is in L!
Definition: A language \(L\) is recursive if there exists a TM \(M\) such that \(L = L(M)\) and \(M\) halts on every \(w \in \Sigma^+\). Thus, A language \(L\) is recursive if and only if there exists a membership algorithm for it.
[Note the difference beteen a recursive language (one that is recognized by a TM) and a recursive algorithm (which merely means that it calls itself).]
NOTE: We will ignore the empty string. In Chapter 9, the definition of the TM assumes that the input string is always padded on both sides of the input. If the input could be a blank, the tape head would not know where the input string was. It would be easy to adjust the definition to include the empty string, but for now we will just examine languages that do not include \(\lambda\).
Note
Not a problem if we use a one-sided tape as our base definition, which is a good argument for doing it that way.
1.1. Enumeration procedure for recursive languages¶
To enumerate all \(w \in \Sigma^+\) in a recursive language \(L\):
1.2. Enumeration procedure for recursively enumerable languages¶
The above procedure does not work, since \(M\) might not halt on strings that are not in the language.
To enumerate all \(w \in \Sigma^+\) in a recursively enumerable language \(L\):
Questions:
- Are there languages that are RE but not recursive? yes.
- Are there languages that are not RE? yes
We will prove that there is a language that is not recursively enumerable.
Note
Ask what is a powerset. \(2^{\{a,b\}}, 2^{pos. int.}\)
Theorem 1
Theorem: Let \(S\) be an infinite countable set. Its powerset \(2^S\) is not countable.
Proof: Use diagonalization
\[\begin{split}\begin{array}{c|cccccccc} & s_1 & s_2 & s_3 & s_4 & s_5 & s_6 & s_7 & ... \\ \hline t_1 & \underline{0} & 1 & 0 & 1 & 0 & 0 & 1 & ... \\ t_2 & 1 & \underline{1} & 0 & 0 & 1 & 1 & 0 & ... \\ t_3 & 0 & 0 & \underline{0} & 0 & 1 & 0 & 0 & ... \\ t_4 & 1 & 0 & 1 & \underline{0} & 1 & 1 & 0 & ... \\ t_5 & 1 & 1 & 1 & 1 & \underline{1} & 1 & 1 & ... \\ t_6 & 1 & 0 & 0 & 1 & 0 & \underline{0} & 1 & ... \\ t_7 & 0 & 1 & 0 & 1 & 0 & 0 & \underline{0} & ... \\ ... & \\ \\ \hline \hline \hat{t} & 1 & 0 & 1 & 1 & 0 & 1 & 1 & ...\\ \end{array}\end{split}\]
Theorem 2
Theorem: For any nonempty \(\Sigma\), there exist languages that are not recursively enumerable.
Proof:
Theorem 3
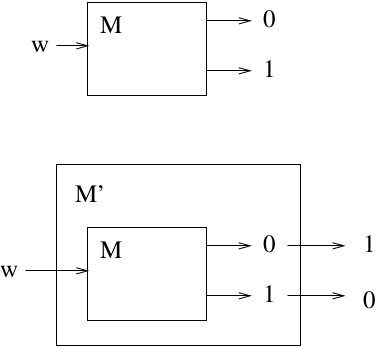
Theorem: There exists a recursively enumerable language \(L\) such that \(\bar L\) is not recursively enumerable.
Proof:
The next two theorems in conjunction with the previous theorem will show that there are some languages that are recursively enumerable, but not recursive.
Theorem 4
Theorem: If languages \(L\) and \(\bar{L}\) are both RE, then L is recursive.
Proof:
Theorem 5
Theorem: If \(L\) is recursive, then \(\bar{L}\) is recursive.
Proof:
If \(L\) is not recursive, then neither \(L\) nor \(\bar{L}\) can be RE.
The language \(L = \{ a^i | a^i \in L(M_i) \}\) is RE but not recursive (since we proved that its complement was not RE).
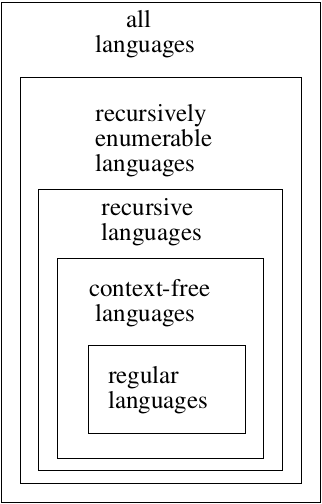
Hierarchy of Languages:
Now we will look at the grammar that represents the same language as the turing machine.
Note
Also mention DCFL (which is between reg and CFL), CS (which is between CFL and REC)
Definition: A grammar \(G = (V,T,S,P)\) is unrestricted if all productions are of the form
\(u \rightarrow v\)
where \(u \in (V \cup T)^+\) and \(v \in (V \cup T)^*\).
No conditions are imposed on the productions. You can have any number of variables and terminals on the left hand side.
Example 1
Let \(G = (\{S,A,X\}, \{a,b\},S,P), P =\)
\(S \rightarrow bAaaX\)\(bAa \rightarrow abA\)\(AX \rightarrow \lambda\)
A derivation of \(aab\) is: (the left hand side that is replaced is underlined)
\(S \Rightarrow \underline{bAa}aX \Rightarrow a\underline{bAa}X \Rightarrow aab\underline{AX} \Rightarrow aab\)
Example 2
Find an unrestricted grammar \(G\) such that \(L(G) = \{a^nb^nc^n | n> 0\}\)
\(G = (V,T,S,P)\)
\(V = \{S,A,B,D,E,X\}\)
\(T = \{a,b,c\}\)
\(P =\)
Change the last rule to \(DX \rightarrow c\) and you can derive the string \(aaabbcbcc\), moves a \(c\) in the wrong place to the end of the string...
To derive string \(aaabbbccc\), use productions 1, 2 and 3 to generate a string that has the correct number of a's b's and c's. The a's will all be together, but the b's and c's will be intertwined.
\(S \Rightarrow AX \Rightarrow aAbcX \Rightarrow aaAbcbcX \Rightarrow aaaBbcbcbcX\)
Use a \(B\) to move right through a group of \(B\) 's until it sees a \(c\). Replace the \(c\) by a \(D\), and use the \(D\) to move right to the end of the string. Then write the \(c\) at the end of the string. Use an \(E\) to move back to the left.
\(aaaBbcbcbcX \Rightarrow aaabBcbcbcX \Rightarrow aaabDbcbcX\)\(\Rightarrow aaabbDcbcX \Rightarrow aaabbcDbcX \Rightarrow aaabbcbDcX\)\(\Rightarrow aaabbcbcDX \Rightarrow aaabbcbcEXc\)\(\Rightarrow aaabbcbEcXc\)\(\stackrel{*}{\Rightarrow} aaaEbbcbcXc \Rightarrow aaaBbbcbcXc\)
Repeat this process until all the \(c\) 's have been moved to the end of the string. Then remove the \(X\) from the string.
\(aaaBbbcbcXc \stackrel{*}{\Rightarrow} aaaBbbbXccc \stackrel{*}{\Rightarrow} aaabbbBXccc \Rightarrow aaabbbccc\)
Theorem 6
Theorem: If \(G\) is an unrestricted grammar, then \(L(G)\) is recursively enumerable.
Proof:
List all strings that can be derived in one step.
\(S \Rightarrow w\)
List all strings that can be derived in two steps.
\(S \Rightarrow x \Rightarrow w\)
List all strings that can be derived in three steps.
etc.
It is possible to enumerate all strings in the language.
Theorem 7
Theorem: If \(L\) is recursively enumerable, then there exists an unrestricted grammar \(G\) such that \(L = L(G)\).
Proof: (Sketch!)
L is recursively enumerable.\(\Rightarrow\) there exists a TM \(M\) such that \(L(M) = L\).\(M = (Q, \Sigma, \Gamma, \delta, q_0, B, F)\)Idea \(M\) starts with \(w\) and eventually ends up with a final state.\(q_0w \stackrel{*}{\vdash} x_1q_fx_2\) for some \(q_f \in F, x_1, x_2 \in \Gamma^*\)Construct an unrestricted grammar \(G\) such that \(L(G) = L(M)\).But in \(G\), grammar starts with \(S\) and eventually derives \(w\), \(S \stackrel{*}{\Rightarrow}w\)So the constructed grammar will mimic the Turing machine in reverse.Three steps:1. \(S \stackrel{*}{\Rightarrow} B \ldots B\#xq_fyB\ldots B\)with \(x, y \in \Gamma^*\) for every possible combination2. \(B \ldots B\#xq_fyB\ldots B \stackrel{*}{\Rightarrow} B\ldots B\#q_0wB\ldots B\)by following rules that mimic transitions in reverse order.3. \(B\ldots B\#q_0wB\ldots B \stackrel{*}{\Rightarrow} w\)Here just remove the blanks, and \(\# q_0\).So here is the constructed grammar.\(G = (V,T,S,P)\)\(T = \Sigma\)\(V = \{\Gamma - \Sigma\} \cup Q \{\#\} \cup \{S,A\}\)\(P\) for each of the three above are:1. For \(S\stackrel{*}{\Rightarrow}B\ldots B\#xq_fyB\ldots B\)\(S \rightarrow BS \mid SB \mid \#A\)Replace \(S\) with lots of blanks and then finally a #`\(A \rightarrow aA \mid Aa \mid q\)(for every \(a \in \Gamma\) and \(q \in F\))then generate the strings of symbols finishing off with a final state.2. For \(B\ldots B\# xq_fyB\ldots B \stackrel{*}{\Rightarrow} B\ldots B\# q_0wB\ldots B\)Create the rules that mimic what the TM does in reverse order.Mimic left and right moves.For each \(\delta(q_i,a) = (q_j,b,R)\)Add to \(P\), \(bq_j \rightarrow q_ia\)For each \(\delta(q_i,a)=(q_j,b,L)\)add to \(P\), \(q_jcb \rightarrow cq_ia\) for every\(c \in \Gamma\).3. For \(B\ldots B\# q_0wB\ldots B \stackrel{*}{\Rightarrow} w\)To get rid of \(\# q_0\) and blanks,\(\# q_0 \rightarrow \lambda\)\(B \rightarrow \lambda\)Then show that \(S \stackrel{*}{\Rightarrow} w\) iff \(q_0w \stackrel{*}{\vdash} x_1q_fx_2\) for \(q_f \in F\)
Definition: A grammar \(G\) is context-sensitive if all productions are of the form
\(x \rightarrow y\)
where \(x,y \in (V \cup T)^{+}\) and \(|x|\le |y|\)
Can be shown that another way to define these is that all productions are of the form:
\(xAy \rightarrow xvy\)
This is equivalent to saying \(A \rightarrow v\) can be applied in the context of \(x\) on the left and \(x\) on the right.
Definition: \(L\) is context-sensitive (CSL) if there exists a context-sensitive grammar \(G\) such that \(L = L(G)\) or \(L = L(G) \cup \{\lambda\}\).
In the definition of the grammar, we can't have any lambda rules.
We put \(\lambda\) in there so we can claim that CFL \(\subset\) CSL
Theorem: For every CSL \(L\) not including \(\lambda\), \(\exists\) an LBA \(M\) such that \(L = L(M)\).
Theorem: If \(L\) is accepted by an LBA \(M\), then \(\exists\) CSG \(G\) such that \(L(M) = L(G)\).
Theorem: Every context-sensitive language \(L\) is recursive.
Theorem: There exists a recursive language that is not CSL.
Note
Section 11.3 covers context-sensitive languages (CSL). These languages lie between the context-free languages and the recursive languages. CSL's and LBA's (linear bounded automata) represent the same class of languages.