11.2.2.1. Suggested Reading:¶

• Chapter 16 Sorted Lists from Data Structures and Abstractions with Java, 4th edition by Frank M. Carrano and Timothy Henry

• Java documentation on Lists

11.2.5.1. Sorted List ADT¶

A Sorted List is therefore a collection of elements or Objects in sorted order, where

• the ordering of elements is based on something related to the element’s value or the Object’s “state” (When referring to an Object’s state we mean the values of each of its fields)

• each element is of the same type (through inheritance and polymorphism a List could be used to facilitate some combination of comparable types)

An example of a Sorted List could be a List of names, stored as Strings arranged in alphabetical order. In computing circles we often refer to this as lexicographic or lexical order.

Just like Lists and many other data structures, it would be necessary to implement methods that enable client code to add new elements, remove elements, and track and manage the number of elements in the Sorted List. As you progress through this module you will explore the similarities and differences between Lists and Sorted Lists and their implementations.

11.2.7.1. Write it from scratch¶

One way of implementing a SortedList ADT is to simply write it from scratch. We are already familiar with the List ADT implementation and we can draw from that experience to implement the SortedList ADT. Due to the similarities between the two ADTs we would be able to write most of the methods the same way as for any list. A few specific methods would need to be written differently to ensure that sorted order is preserved, i.e. the list stays in sorted throughout its life and the execution of its methods.

When choosing to write from scratch we have two further choices. Similar to implementing a List ADT we can choose to use one of the following:

• use an array implementation

• use a linked implementation

11.2.7.2. Implement using Composition (Wrapper)¶

This approach uses a List ADT implementation to support the implementation of the SortedList ADT. In this implementation approach the Sorted list makes use of an instance of the List ADT (it has-a list, hence the use of the term Composition), this List ADT instance is set up as a field of SortedList, SortedList then acts as client code, calling and managing the use of the list methods in service of SortedList operations. This will be elaborated upon in further detail later on in the module.

11.2.7.3. Implement using Inheritance¶

This approach also uses a List ADT implementation to support the implementation of the SortedList ADT, this time through an is-a or inheritance relationship.

Since we can think of a SortedList as a List with modified characteristics and additional “Sort” logic we can therefore conclude that a SortedList is-a List, thus deriving the benefits of inheritance. The List becomes a parent class, while the SortedList becomes a child of List, inheriting methods from the parent class. Since some SortedList methods must behave differently when compared against their List ADT counterparts we must override these methods when defining the SortedList class. Specifically we must override any methods that do not serve to preserve sorted order. For example methods like add(int newPosition, T newEntry) and replace(givenPosition,newEntry) offer client code control over the positioning of newEntries, this is not appropriate as this could affect the sorted order of the SortedList. The add(newEntry) method would also need to be modified. Further the SortedList would require features not present within the List, requiring us to add these new methods, examples of such include the SortedList ADT methods remove(anEntry) and getPosition(anEntry).

Follow Along, Practice and Explore

Download to run and explore the corresponding project from the video on your own in eclipse. The project CS-GraphWindowLib is required for the sample project above. It is also used in your course projects. To download the CS-GraphWindowLib you must first complete the configuration steps for your first lab. You will then be able to download it via eclipse using the blue down arrow icon or using the Project Menu and selecting “Download Assignment…”

exSortedLists.zip

11.2.10.1. Implementation from Scratch¶

The worst case-efficiencies of the operations on the ADT List and ADT Sorted List have been provided below for both the Array-Based and Linked implementations. Review each table, note the similarities and differences, then consider how implementation details could affect the efficiencies of the various methods.

The table below depicts the worst-case efficiencies of the operations on the ADT sorted list for two implementations

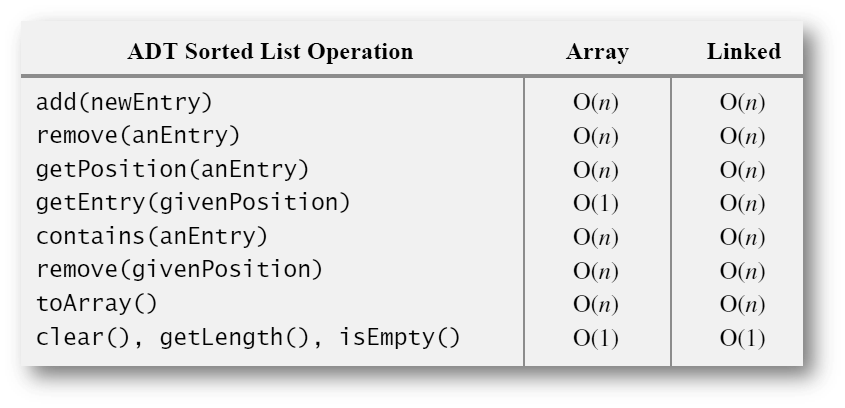
Figure 11.2.1: The worst-case efficiencies of the operations on the sorted list ADT for two implementations (credit: FIGURE 16-5 from course text: Carrano & Henry. Data Structures & Abstractions with Java)¶

The table below depicts the worst-case efficiencies of select ADT List operations for two implementations

Figure 11.2.2: The worst-case efficiencies of the operations on the list ADT for two implementations. (credit FIGURE 16-8 from course text: Carrano & Henry. Data Structures & Abstractions with Java)¶

11.2.10.2. Reflecting upon Efficiencies¶

Consider, for example, the new SortedList ADT method getPosition(…).

The getPosition(…) method receives anEntry as a parameter, then searches the entire list to locate the position of anEntry within the list. In its most basic implementation the getPosition(...) method uses a linear search to locate anEntry within the list, with the content of each position within the list compared against anEntry until either anEntry is found or all positions checked.

Upon finding anEntry the method returns the integer position of the first or only occurrence of anEntry within the list. If the search does not find anEntry within the list the method then returns an integer whose value indicates that anEntry was not found within the list. There are many ways to set this value to indicate anEntry was not found, some developers return an invalid position, for example -1, as a flag to indicate an unsuccessful search. Others may choose instead to return a value greater than the number of entries in the list, while some favor returning the position where anEntry would occur in the list if present, but as a negative integer.

Not that the current efficiency of that method is $O(n)$ for both an Array-based and Linked implementation. This is to be expected, since the list has n elements, then a linear search of the list for anEntry would naturally require all n elements to be checked.

However this is not the most efficient option. The efficiency of this method could be improved by using the fact that the SortedList is in sorted order. Instead of traversing the entire list in search of anEntry the method could stop the search once past where the element should be, if the search encounters an element greater than anEntry before finding anEntry then the method can determine that anEntry is not in the list. The getPosition() method can be further improved by using a binary search instead of a linear search.

11.2.12.1. Efficiency of the Composition Approach¶