5.2. Properties¶
5.2.1. Properties and Proving: Problem 1¶
Consider the property Replace_one_a_with_b or R1awb for short. If L is regular, prove that R1awb(L) is regular.
The property R1awb applied to a language L replaces one a in each string with one b. If a string does not have an a, then the string is not in R1awb(L).
What does this mean? What are we trying to prove?
Example 1: Consider L={aaab,bbaa}
IS L REGULAR? YES, you can apply the property.
R1awb(L)={baab,abab,aabb,bbba,bbab}
Example 2: Consider Σ={a,b}, L={w∈Σ∗∣w has an even number of a′s and an even number of b′s}
Is L regular? YES, How do you know? We built a DFA for this language.
R1awb(L)={w∈Σ∗∣w has an odd number of a′s and an odd number of b′s}
Proof:
5.2.2. Properties and Proving - Problem 2¶
Consider the property Truncate_all_preceeding_b's or TruncPreb for short. If L is regular, prove TruncPreb(L) is regular.
The property TruncPreb applied to a language L removes all preceeding b's in each string. If a string does not have an preceeding b, then the string is the same in TruncPreb(L).
What does this mean? What are we trying to prove?
Example 1: Consider L={aaab,bbaa}
IS L REGULAR? YES, you can apply the property.
TruncPreb(L)={aaab,aa}
Example 2: Consider L={(bba)n∣n>0}
Is L regular? YES. How do you know? We built a DFA for this language.
Note
List out possible strings in the language
TruncPreb(L)={a(bba)n∣n≥0}
Proof:
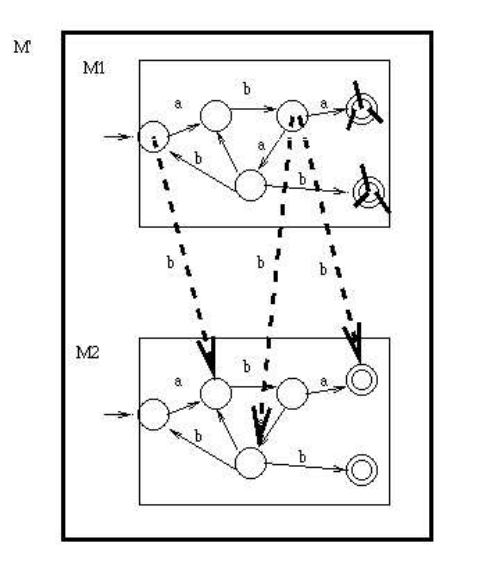
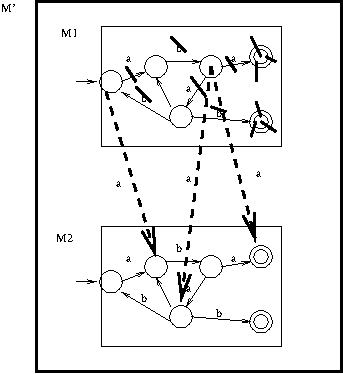
Make a copy of the DFA. For each a arc in the first copy, remove it and instead have the a arc go to the corresponding destination below.
For each b arc in the first copy, change the b to lambda.