16.10. Failure Policies and Garbage Collection¶
At some point during processing, a memory manager could encounter a request for memory that it cannot satisfy. In some situations, there might be nothing that can be done: There simply might not be enough free memory to service the request, and the application may require that the request be serviced immediately. In this case, the memory manager has no option but to return an error, which could in turn lead to a failure of the application program. However, in many cases there are alternatives to simply returning an error. The possible options are referred to collectively as failure policies.
In some cases, there might be sufficient free memory to satisfy the request, but it is scattered among small blocks. This can happen when using a sequential-fit memory allocation method, where external fragmentation has led to a series of small blocks that collectively could service the request. In this case, it might be possible to compact memory by moving the reserved blocks around so that the free space is collected into a single block. A problem with this approach is that the application must somehow be able to deal with the fact that all of its data have now been moved to different locations. If the application program relies on the absolute positions of the data in any way, this would be disastrous. One approach for dealing with this problem is the use of handles. A handle is a second level of indirection to a memory location. The memory allocation routine does not return a pointer to the block of storage, but rather a pointer to a variable that in turn points to the storage. This variable is the handle. The handle never moves its position, but the position of the block might be moved and the value of the handle updated. This figure illustrates the concept.
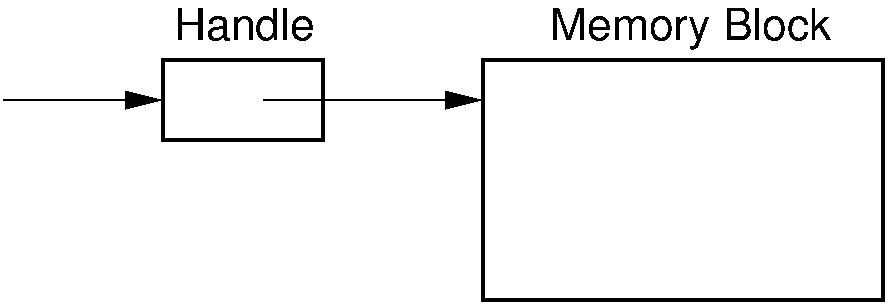
Figure 16.10.1: Using handles for dynamic memory management. The memory manager returns the address of the handle in response to a memory request. The handle stores the address of the actual memory block. In this way, the memory block might be moved (with its address updated in the handle) without disrupting the application program.
Another failure policy that might work in some applications is to defer the memory request until sufficient memory becomes available. For example, a multitasking operating system could adopt the strategy of not allowing a process to run until there is sufficient memory available. While such a delay might be annoying to the user, it is better than halting the entire system. The assumption here is that other processes will eventually terminate, freeing memory.
Another option might be to allocate more memory to the memory
manager.
In a zoned memory allocation system where the memory
manager is part of a larger system, this might be a viable option.
In a C++ program that implements its own memory manager, it might be
possible to get more memory from the system-level new operator,
such as is done by a freelist.
The last failure policy that we will consider is garbage collection. Consider the following series of statements.:
Integer p = new Integer[5];
Integer q = new Integer[10];
p = q;
In some languages, such as C++, this would be considered
bad form because the original space allocated to p
is lost as a result of the third assignment.
This space cannot be used again by the program.
Such lost memory is referred to as garbage, also known as a
memory leak.
When no program variable points to a block of space, no
future access to that space is possible.
Of course, if another variable had first been assigned to point to
p 's space, then reassigning p would not create garbage.
Some programming languages take a different view towards garbage.
In particular, the LISP programming language uses a multilist
representation, and all storage is in the form
either of internal nodes with two pointers or atoms.
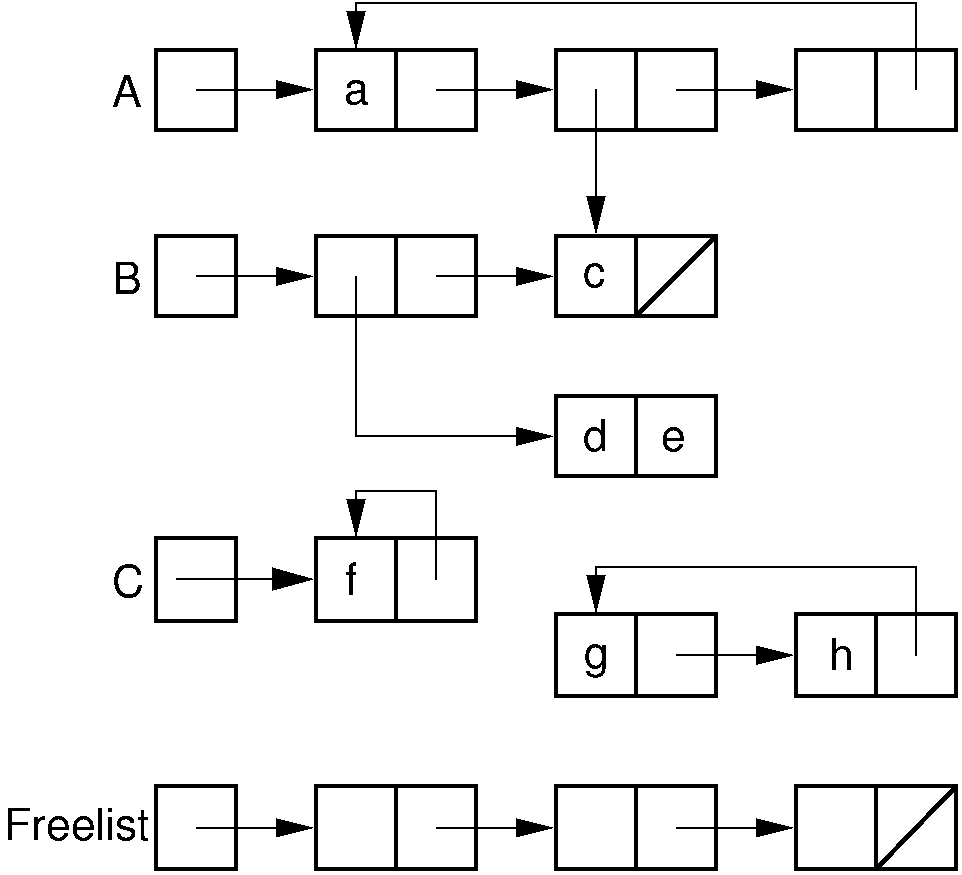
The figure below shows a typical collection of LISP structures,
headed by variables named A, B, and C,
along with a freelist.
In LISP, list objects are constantly being put together in various ways as temporary variables, and then all reference to them is lost when the object is no longer needed. Thus, garbage is normal in LISP, and in fact cannot be avoided during normal processing. When LISP runs out of memory, it resorts to a garbage collection process to recover the space tied up in garbage. Garbage collection consists of examining the managed memory pool to determine which parts are still being used and which parts are garbage. In particular, a list is kept of all program variables, and any memory locations not reachable from one of these variables are considered to be garbage. When the garbage collector executes, all unused memory locations are placed in free store for future access. This approach has the advantage that it allows for easy collection of garbage. It has the disadvantage, from a user's point of view, that every so often the system must halt while it performs garbage collection. For example, garbage collection is noticeable in the Emacs text editor, which is normally implemented in LISP. Occasionally the user must wait for a moment while the memory management system performs garbage collection.
The Java programming language also makes use of garbage collection. As in LISP, it is common practice in Java to allocate dynamic memory as needed, and to later drop all references to that memory. The garbage collector is responsible for reclaiming such unused space as necessary. This might require extra time when running the program, but it makes life considerably easier for the programmer. In contrast, many large applications written in C++ (even commonly used commercial software) contain memory leaks that will in time cause the program to fail.
Several algorithms have been used for garbage collection. One is the reference count algorithm. Here, every dynamically allocated memory block includes space for a count field. Whenever a pointer is directed to a memory block, the reference count is increased. Whenever a pointer is directed away from a memory block, the reference count is decreased. If the count ever becomes zero, then the memory block is considered garbage and is immediately placed in free store. This approach has the advantage that it does not require an explicit garbage collection phase, because information is put in free store immediately when it becomes garbage.
The reference count algorithm is used by the Unix file system. Files can have multiple names, called links. The file system keeps a count of the number of links to each file. Whenever a file is "deleted", in actuality its link field is simply reduced by one. If there is another link to the file, then no space is recovered by the file system. Whenever the number of links goes to zero, the file's space becomes available for reuse.
Reference counts have several major disadvantages. First, a reference count must be maintained for each memory object. This works well when the objects are large, such as a file. However, it will not work well in a system such as LISP where the memory objects typically consist of two pointers or a value (an atom). Another major problem occurs when garbage contains cycles. Consider the figure below. Here each memory object is pointed to once, but the collection of objects is still garbage because no pointer points to the collection. Thus, reference counts only work when the memory objects are linked together without cycles, such as the Unix file system where files can only be organized as a Directed Acyclic Graph.
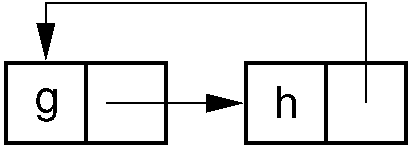
Figure 16.10.3: Garbage cycle example. All memory elements in the cycle have non-zero reference counts because each element has one pointer to it, even though the entire cycle is garbage.
Another approach to garbage collection is the mark/sweep algorithm. Here, each memory object needs only a single mark bit rather than a reference counter field. When free store is exhausted, a separate garbage collection phase takes place as follows.
- Clear all mark bits.
- Perform depth-first search (DFS) following pointers from each variable on the system's list of variables. Each memory element encountered during the DFS has its mark bit turned on.
- .# A "sweep" is made through the memory pool, visiting all elements.
- Unmarked elements are considered garbage and placed in free store.
The advantages of the mark/sweep approach are that it needs less space than is necessary for reference counts, and it works for cycles. However, there is a major disadvantage. This is a "hidden" space requirement needed to do the processing. DFS is a recursive algorithm: Either it must be implemented recursively, in which case the compiler's runtime system maintains a stack, or else the memory manager can maintain its own stack. What happens if all memory is contained in a single linked list? Then the depth of the recursion (or the size of the stack) is the number of memory cells! Unfortunately, the space for the DFS stack must be available at the worst conceivable time, that is, when free memory has been exhausted.
Fortunately, a clever technique allows DFS to be performed without requiring additional space for a stack. Instead, the structure being traversed is used to hold the stack. At each step deeper into the traversal, instead of storing a pointer on the stack, we "borrow" the pointer being followed. This pointer is set to point back to the node we just came from in the previous step, as illustrated by the figure below. Each borrowed pointer stores an additional bit to tell us whether we came down the left branch or the right branch of the link node being pointed to. At any given instant we have passed down only one path from the root, and we can follow the trail of pointers back up. As we return (equivalent to popping the recursion stack), we set the pointer back to its original position so as to return the structure to its original condition. This is known as the Deutsch-Schorr-Waite garbage collection algorithm.
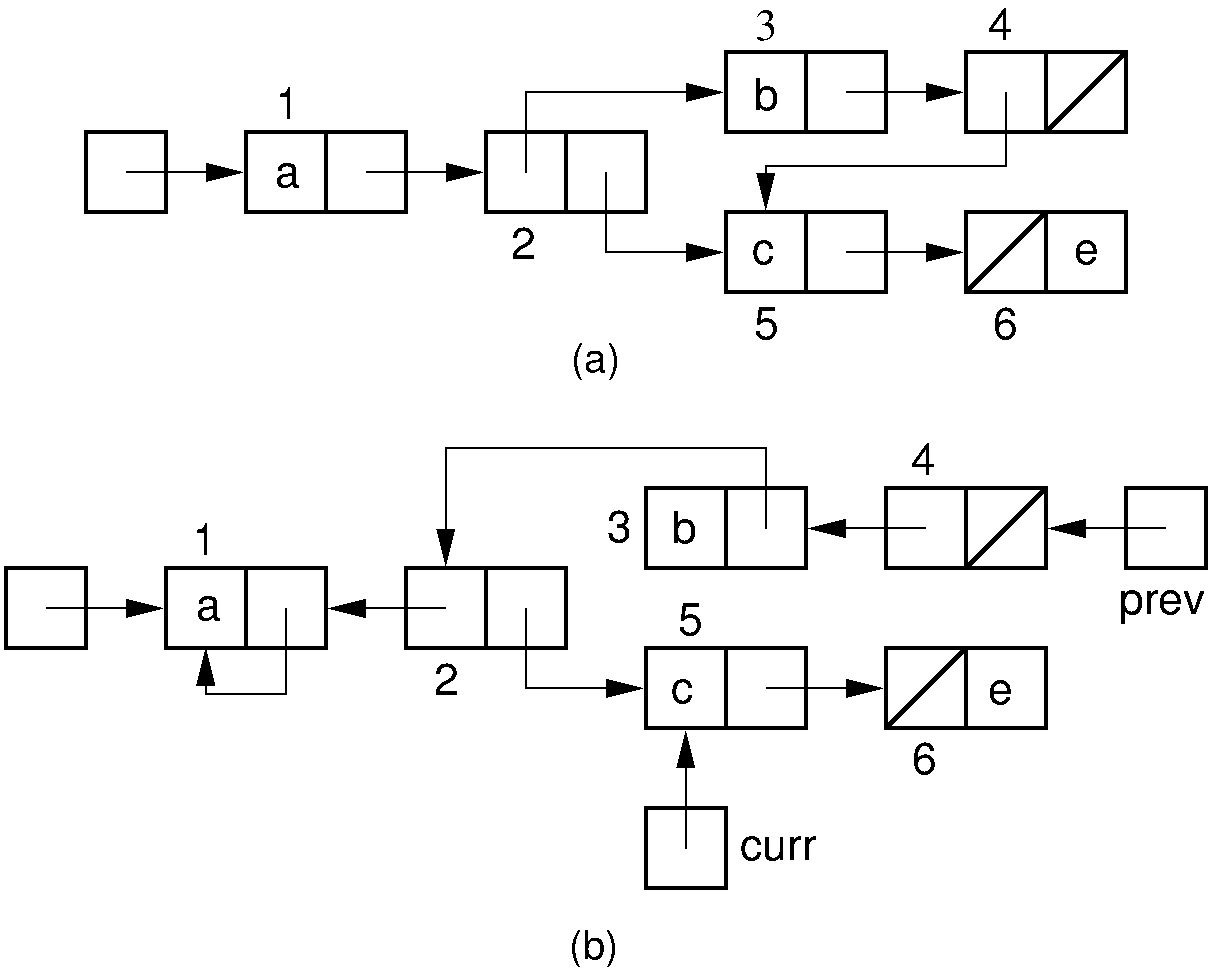
Figure 16.10.4: Example of the Deutsch-Schorr-Waite garbage collection
algorithm.
(a) The initial multilist structure.
(b) The multilist structure of (a) at the instant when link node 5 is
being processed by the garbage collection algorithm.
A chain of pointers stretching from variable prev to the head
node of the structure has been (temporarily) created by the garbage
collection algorithm.