Let's look at a visualization to explain why the cost for buildheap is $\theta(n)$. We will use an example with 31 records in the heap. This means that there are 16 leaf nodes and 15 internal nodes.
Here is the process for removing the maximum value from the max heap. We know that this value is at the root (array position 0), but we also need to update the heap when we remove it.
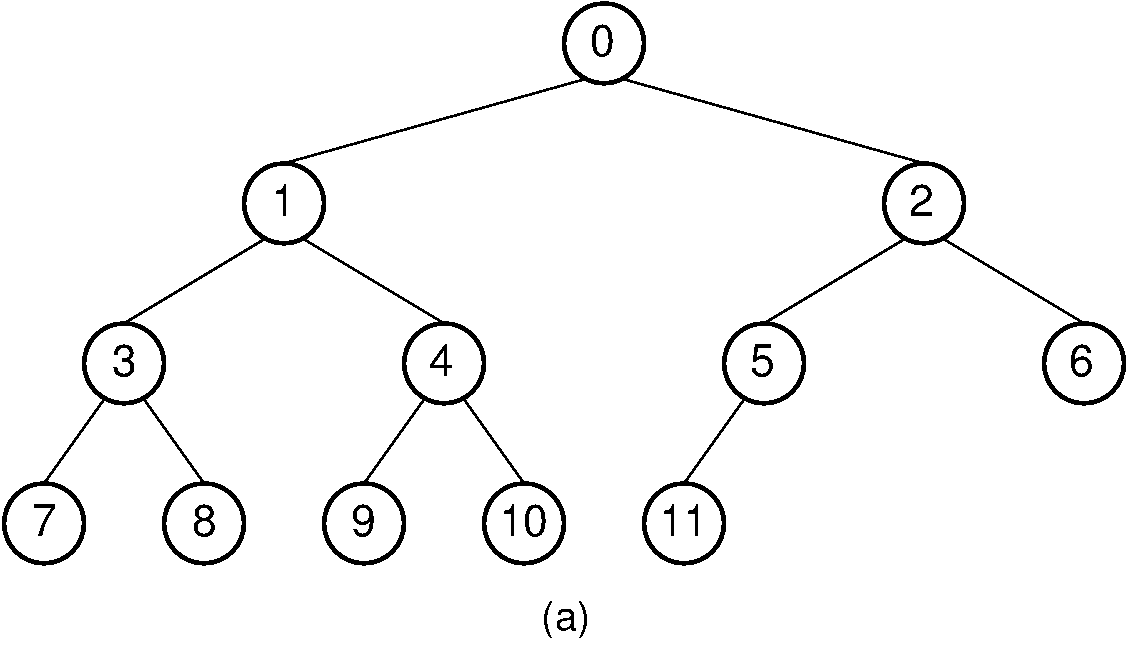
Position01234567891011Parent−−00112233445Left Child1357911−−−−−−−−−−−−Right Child246810−−−−−−−−−−−−−−Left Sibling−−−−1−−3−−5−−7−−9−−Right Sibling−−2−−4−−6−−8−−10−−−−
