30.7.1.1. Algorithm Efficiency¶

There are often many approaches (algorithms) to solve a problem. How do we choose between them?

At the heart of computer program design are two (sometimes conflicting) goals.

1. To design an algorithm that is easy to understand, code, debug.
2. To design an algorithm that makes efficient use of the computer’s resources.

Goal (1) is the concern of Software Engineering

Goal (2) is the concern of data structures and algorithm analysis

30.7.1.2. How to Measure Efficiency?¶

1. Empirical comparison (run programs)
2. Asymptotic Algorithm Analysis

• Critical resources:
• Factors affecting running time:
• For most algorithms, running time depends on “size” of the input.
• Running time is expressed as $\mathbf{T}(n)$ for some function $\mathbf{T}$ on input size $n$.

30.7.1.3. Problems, Algorithms, Programs¶

1 / 16 Settings

<<<>>>

Searching Problem

1. Key 10
2. Key 21
3. Key 32
4. Key 43
5. Key 54
6. Key 65

Target key

Found

Not found

Index of the target key

$n$

1. 50
2. 21
3. 32
4. 93
5. 104
6. 85

Target key = 9

Saving...
Server Error
Resubmit

30.7.1.4. Growth Rate Example (1)¶

Example 1: Find largest value

• Java
• Processing
• Java (Generic)
• C++

// Return position of largest value in integer array A
static int largest(int[] A) {
  int currlarge = 0;             // Position of largest element seen
  for (int i=1; i<A.length; i++) // For each element
    if (A[currlarge] < A[i])     //   if A[i] is larger
       currlarge = i;            //     remember its position
  return currlarge;              // Return largest position
}

// Return position of largest value in integer array A
int largest(int[] A) {
  int currlarge = 0;             // Position of largest element seen
  for (int i=1; i<A.length; i++) // For each element
    if (A[currlarge] < A[i])     //   if A[i] is larger
       currlarge = i;            //     remember its position
  return currlarge;              // Return largest position
}

// Return position of largest value in integer array A
static int largest(int[] A) {
  int currlarge = 0;             // Position of largest element seen
  for (int i=1; i<A.length; i++) // For each element
    if (A[currlarge] < A[i])     //   if A[i] is larger
       currlarge = i;            //     remember its position
  return currlarge;              // Return largest position
}

/** Return position of largest value in integer array A */
int largest(int A[], int size) {
  int currlarge = 0;             // Position of largest element seen
  for (int i=1; i<size; i++)     // For each element
    if (A[currlarge] < A[i])     //   if A[i] is larger
       currlarge = i;            //     remember its position
  return currlarge;              // Return largest position
}

30.7.1.5. Growth Rate Example (2)¶

Example 2: Assignment statement

Example 3: Double loop

• Java
• Processing
• Java (Generic)
• C++

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

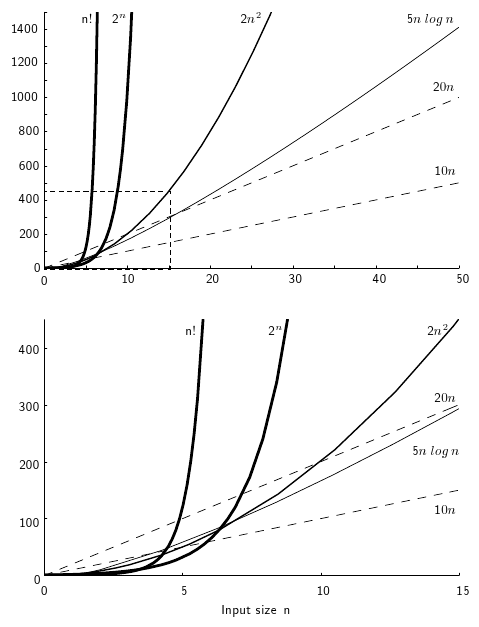
30.7.1.6. Growth Rate Graph¶

30.7.1.7. Best, Worst, Average Cases¶

Not all inputs of a given size take the same time to run.

Sequential search for K in an array of $n$ integers:

• Begin at first element in array and look at each element in turn until K is found

Best case:

Worst case:

Average case:

30.7.1.8. Which Analysis to Use?¶

• While average time appears to be the fairest measure, it may be difficult to determine.
• When is the worst case time important?

30.7.1.9. Faster Computer or Algorithm?¶

Suppose we buy a computer 10 times faster.

• n: size of input that can be processed in one second on old computer (in 1000 computational units)
• n’: size of input that can be processed in one second on new computer (in 10,000 computational units)

30.7.1.10. Faster Computer or Algorithm? 2¶

$$\begin{split}\begin{array} {l|r|r|l|r} \mathbf{f(n)} & \mathbf{n} & \mathbf{n'} & \mathbf{Change} & \mathbf{n'/n}\\ \hline 10n & 1000 & 10,000 & n' = 10n & 10\\ 20n & 500 & 5000 & n' = 10n & 10\\ 5 n \log n & 250 & 1842 & \sqrt{10} n < n' < 10n & 7.37\\ 2 n^2 & 70 & 223 & n' = \sqrt{10} n & 3.16\\ 2^n & 13 & 16 & n' = n + 3 & --\\ \end{array}\end{split}$$

30.7.1.11. Asymptotic Analysis: Big-oh¶

Definition: For $\mathbf{T}(n)$ a non-negatively valued function, $\mathbf{T}(n)$ is in the set $O(f(n))$ if there exist two positive constants $c$ and $n_0$ such that $T(n) \leq cf(n)$ for all $n > n_0$.

Use: The algorithm is in $O(n^2)$ in [best, average, worst] case.

Meaning: For all data sets big enough (i.e., $n>n_0$), the algorithm always executes in less than $cf(n)$ steps in the [best, average, worst] case.

30.7.1.12. Big-oh Notation (cont)¶

Big-oh notation indicates an upper bound.

Example: If $\mathbf{T}(n) = 3n^2$ then $\mathbf{T}(n)$ is in $O(n^2)$.

Look for the tightest upper bound:

• While $\mathbf{T}(n) = 3n^2$ is in $O(n^3)$, we prefer $O(n^2)$.

30.7.1.13. Big-Oh Examples¶

Example 1: Finding value X in an array (average cost).

Then $\textbf{T}(n) = c_{s}n/2$.

For all values of $n > 1, c_{s}n/2 \leq c_{s}n$.

Therefore, the definition is satisfied for $f(n)=n, n_0 = 1$, and $c = c_s$. Hence, $\textbf{T}(n)$ is in $O(n)$.

30.7.1.14. Big-Oh Examples (2)¶

Example 2: Suppose $\textbf{T}(n) = c_{1}n^2 + c_{2}n$, where $c_1$ and $c_2$ are positive.

$c_{1}n^2 + c_{2}n \leq c_{1}n^2 + c_{2}n^2 \leq (c_1 + c_2)n^2$ for all $n > 1$.

Then $\textbf{T}(n) \leq cn^2$ whenever $n > n_0$, for $c = c_1 + c_2$ and $n_0 = 1$.

Therefore, $\textbf{T}(n)$ is in $O(n^2)$ by definition.

Example 3: $\textbf{T}(n) = c$. Then $\textbf{T}(n)$ is in $O(1)$.

30.7.1.15. A Common Misunderstanding¶

“The best case for my algorithm is n=1 because that is the fastest.”

WRONG!

Big-oh refers to a growth rate as n grows to $\infty$

Best case is defined for the input of size n that is cheapest among all inputs of size $n$.

30.7.1.16. Big-Omega $\Omega$¶

Definition: For $\textbf{T}(n)$ a non-negatively valued function, $\textbf{T}(n)$ is in the set $\Omega(g(n))$ if there exist two positive constants $c$ and $n_0$ such that $\textbf{T}(n) \geq cg(n)$ for all $n > n_0$.

Meaning: For all data sets big enough (i.e., $n > n_0$), the algorithm always requires more than $cg(n)$ steps.

Lower bound.

30.7.1.17. Big-Omega Example¶

$\textbf{T}(n) = c_1n^2 + c_2n$.

$c_1n^2 + c_2n \geq c_1n^2$ for all $n > 1$.

$\textbf{T}(n) \geq cn^2$ for $c = c_1$ and $n_0 = 1$.

Therefore, $\textbf{T}(n)$ is in $\Omega(n^2)$ by the definition.

We want the greatest lower bound.

30.7.1.18. Theta Notation $\Theta$¶

When big-Oh and $\Omega$ coincide, we indicate this by using $\Theta$ (big-Theta) notation.

Definition: An algorithm is said to be in $\Theta(h(n))$ if it is in $O(h(n))$ and it is in $\Omega(h(n))$.

30.7.1.19. A Common Misunderstanding¶

Confusing worst case with upper bound.

Upper bound refers to a growth rate.

Worst case refers to the worst input from among the choices for possible inputs of a given size.

30.7.1.20. Simplifying Rules¶

1. If $f(n)$ is in $O(g(n))$ and $g(n)$ is in $O(h(n))$, then $f(n)$ is in $O(h(n))$.
2. If $f(n)$ is in $O(kg(n))$ for some constant $k > 0$, then $f(n)$ is in $O(g(n))$.
3. If $f_1(n)$ is in $O(g_1(n))$ and $f_2(n)$ is in $O(g_2(n))$, then $(f_1 + f_2)(n)$ is in $O(\max(g_1(n), g_2(n)))$.
4. If $f_1(n)$ is in $O(g_1(n))$ and $f_2(n)$ is in $O(g_2(n))$, then $f_1(n)f_2(n)$ is in $O(g_1(n)g_2(n))$.

30.7.1.21. Summary¶

Costs for all inputs of an arbitrary (but fixed) size $n$ for three representative algorithms

$I_n$

cheap

expensive

$2^n-1$

_

$*$

Towers of Hanoi

$I_n$

cheap

expensive

$n$

_

FindMax

$I_n$

cheap

expensive

$n$

_

$1$

_

Find

Costs, as $n$ grows, for some representative algorithms

$n$

cheap

expensive

$2^n-1$

_

$T(n) = 2^n-1$

Towers of Hanoi

$n$

cheap

expensive

$n$

_

$1$

_

FindMax

$n$

cheap

expensive

$1$

_

Find (Best)

$n$

cheap

expensive

$n$

_

$1$

_

Find (Average)

$n$

cheap

expensive

$n$

_

$1$

_

Find (Worst)

30.7.1.22. .¶

.

30.7.1.23. Time Complexity Examples (1)¶

Example: a = b;

This assignment takes constant time, so it is $\Theta(1)$.

Example:

• Java
• Processing
• Java (Generic)
• C++

sum = 0;
for (i=1; i<=n; i++)
   sum += n;

sum = 0;
for (i=1; i<=n; i++)
   sum += n;

sum = 0;
for (i=1; i<=n; i++)
   sum += n;

sum = 0;
for (i=1; i<=n; i++)
   sum += n;

30.7.1.24. Time Complexity Examples (2)¶

Example:

• Java
• Processing
• Java (Generic)
• C++

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

sum = 0;
for (j=1; j<=n; j++)     // First for loop
   for (i=1; i<=j; i++)  //   is a double loop
      sum++;
for (k=0; k<n; k++)      // Second for loop
   A[k] = k;

30.7.1.25. Time Complexity Examples (3)¶

Example: Compare these two code fragments:

• Java
• Processing
• Java (Generic)
• C++

sum1 = 0;
for (i=1; i<=n; i++)     // First double loop
   for (j=1; j<=n; j++)  //   do n times
      sum1++;

sum2 = 0;
for (i=1; i<=n; i++)     // Second double loop
   for (j=1; j<=i; j++)  //   do i times
      sum2++;

sum1 = 0;
for (i=1; i<=n; i++)     // First double loop
   for (j=1; j<=n; j++)  //   do n times
      sum1++;

sum2 = 0;
for (i=1; i<=n; i++)     // Second double loop
   for (j=1; j<=i; j++)  //   do i times
      sum2++;

sum1 = 0;
for (i=1; i<=n; i++)     // First double loop
   for (j=1; j<=n; j++)  //   do n times
      sum1++;

sum2 = 0;
for (i=1; i<=n; i++)     // Second double loop
   for (j=1; j<=i; j++)  //   do i times
      sum2++;

sum1 = 0;
for (i=1; i<=n; i++)     // First double loop
   for (j=1; j<=n; j++)  //   do n times
      sum1++;

sum2 = 0;
for (i=1; i<=n; i++)     // Second double loop
   for (j=1; j<=i; j++)  //   do i times
      sum2++;

30.7.1.26. Time Complexity Examples (4)¶

Not all double loops are $\Theta(n^2)$.

• Java
• Processing
• Java (Generic)
• C++

sum1 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=n; j++)  // Do n times
      sum1++;

sum2 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=k; j++)  // Do k times
      sum2++;

sum1 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=n; j++)  // Do n times
      sum1++;

sum2 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=k; j++)  // Do k times
      sum2++;

sum1 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=n; j++)  // Do n times
      sum1++;

sum2 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=k; j++)  // Do k times
      sum2++;

sum1 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=n; j++)  // Do n times
      sum1++;

sum2 = 0;
for (k=1; k<=n; k*=2)    // Do log n times
   for (j=1; j<=k; j++)  // Do k times
      sum2++;

30.7.1.27. Binary Search¶

How many elements are examined in worst case?

30.7.1.28. Other Control Statements¶

while loop: Analyze like a for loop.

if statement: Take greater complexity of then/else clauses.

switch statement: Take complexity of most expensive case.

Subroutine call: Complexity of the subroutine.

30.7.1.29. Analyzing Problems¶

Upper bound: Upper bound of best known algorithm.

Lower bound: Lower bound for every possible algorithm.

30.7.1.30. Analyzing Problems: Example¶

May or may not be able to obtain matching upper and lower bounds.

Example of imperfect knowledge: Sorting

1. Cost of I/O: $\Omega(n)$.
2. Bubble or insertion sort: $O(n^2)$.
3. A better sort (Quicksort, Mergesort, Heapsort, etc.): $O(n \log n)$.
4. We prove later that sorting is in $\Omega(n \log n)$.

30.7.1.31. Space/Time Tradeoff Principle¶

One can often reduce time if one is willing to sacrifice space, or vice versa.

• Encoding or packing information

  • Boolean flags

• Table lookup

  • Factorials

Disk-based Space/Time Tradeoff Principle: The smaller you make the disk storage requirements, the faster your program will run.

30.7.1.32. Multiple Parameters¶

Compute the rank ordering for all C pixel values in a picture of P pixels.

• Java
• Processing
• Java (Generic)
• C++

  for (i=0; i<C; i++)   // Initialize count
     count[i] = 0;
  for (i=0; i<P; i++)   // Look at all of the pixels
     count[value(i)]++; // Increment a pixel value count
  sort(count);          // Sort pixel value counts

  for (i=0; i<C; i++)   // Initialize count
     count[i] = 0;
  for (i=0; i<P; i++)   // Look at all of the pixels
     count[value(i)]++; // Increment a pixel value count
  sort(count);          // Sort pixel value counts

  for (i=0; i<C; i++)   // Initialize count
     count[i] = 0;
  for (i=0; i<P; i++)   // Look at all of the pixels
     count[value(i)]++; // Increment a pixel value count
  sort(count);          // Sort pixel value counts

  for (i=0; i<C; i++)   // Initialize count
     count[i] = 0;
  for (i=0; i<P; i++)   // Look at all of the pixels
     count[value(i)]++; // Increment a pixel value count
  sort(count, C);       // Sort pixel value counts

If we use P as the measure, then time is $(P \log P)$.

More accurate is $\Theta(P + C log C)$.

30.7.1.33. Space Complexity¶

Space complexity can also be analyzed with asymptotic complexity analysis.

Time: Algorithm

Space: Data Structure