5.Our Current Model of the FL Universe
Regular Languages:
Regular Grammars
DFA/NFA
Regular Expressions
Context Free Languages:
Context Free Grammars
Implementation?
DFA Review
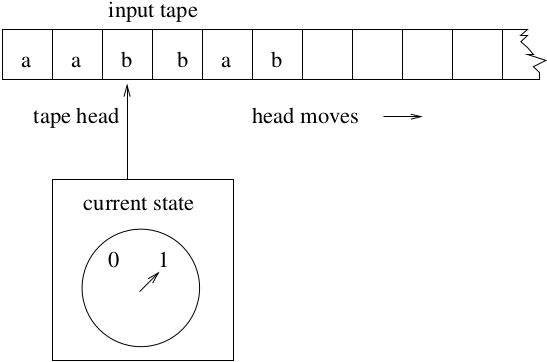
Recall: A DFA \(=(Q, \Sigma, \delta, q_0, F)\).
In a DFA, the tape is read only, the head moves to the right only.
DFAs are limited in power.
They recognize regular languages but cannot recognize many other
“simple” langages like \(a^nb^n\).
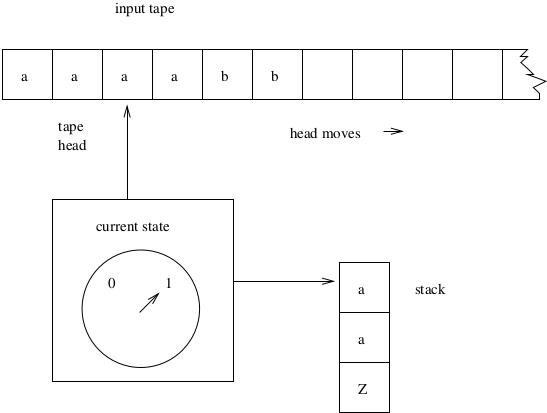
Pushdown Automata
Give the DFA a stack:
This is called a Pushdown Automata (PDA).
Name comes from new ability to push down and
store symbols on stack
Adds memory: The machine stores and retrieves data from the stack
Old limitations still apply: Tape is read only, head moves only to
the right
Non-deterministic PDA (1)
We gave DFAs the concept of nondeterminism:
Multiple edges out of a state on same input condition,
\(\lambda\) transitions
This did not change the set of languages that could be
recognized by DFAs.
For convenience (at the moment), we will also add non-determinism
to PDAs.
Non-deterministic PDA (2)
Definition: A nondeterministic PDA (NPDA) is defined by
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)
\(Q\) is a finite set of states
\(\Sigma\) is the tape (input) alphabet (a finite set)
\(\Gamma\) is the stack alphabet (a finite set)
(\(\Leftarrow\) new)
\(q_0\) is the initial state, \(q_0 \in Q\)
\(z\) is the start stack symbol
(marks the bottom of the stack), \(z \in \Gamma\)
(\(\Leftarrow\) new)
\(F \subseteq Q\) is the set of final states.
\(\delta : Q \times (\Sigma \cup \{\lambda\}) \times \Gamma \rightarrow\)
finite subsets of \(Q \times \Gamma^*\)
<< You need to really pay attention to exactly what is going on with
this transition function notation! >>
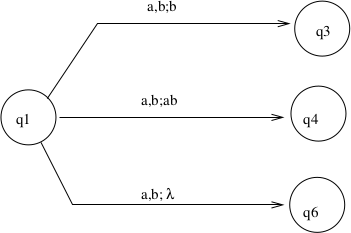
Example of Transitions (1)
\(\delta(q_1, a, b) = \{(q_3, b),(q_4, ab), (q_6, \lambda)\}\)
Meaning: If in state \(q_1\) with \(a\) the current tape
symbol and \(b\) the symbol on top of the stack,
then pop \(b\), and either
move to \(q_3\) and push \(b\) back onto the stack
move to \(q_4\) and push \(ab\) onto stack (\(a\) on top)
move to \(q_6\) (now stack is one character shorter)
\(z\) (the initial stack bottom marker) is priviledged: It
never comes off, stack is never empty.
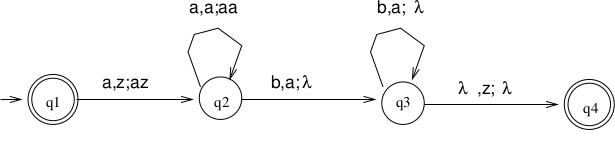
Example of Transitions (2)
Transitions can be represented using a transition diagram.
The diagram for the above transitions is:
Each arc is labeled by a triple \(<x, y, z>\) where \(x\) is
the current input symbol, \(y\) is the top of stack symbol which
is popped from the stack, and \(z\) is a string that is pushed
onto the stack.
<< Warning: What is a character, and what is a string? >>
Instantaneous Descriptions
Instantaneous Description:
\((q, w, u)\)
This describes the current state \(q\),
unread portion of the input string \(w\),
and the current contents of the stack \(u\).
(Like DFA, there is no history for how we got to this.)
This is a configuration in JFLAP.
Description of a Move:
\((q_1, aw, bx) \vdash (q_2, w, yx)\)
is possible if and only iff
\((q_2, y) \in \delta(q_1, a, b)\).
\((q_1, w_1, x_1) \stackrel{*}{\vdash} (q_2, w_2, x_2)\)
indicates possible configuration change over multiple steps.
<< “Possible” because this is non-deterministic >>
Definition for Language Acceptance
Definition: Let \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)
be a NPDA.
\(L(M) = \{w \in \Sigma^* \mid (q_0, w, z) \stackrel{*}{\vdash} (p, \lambda, u), p \in F, u \in \Gamma^*\}\).
The NPDA accepts all strings that start in \(q_0\) and end in a
final state.
NOTE: Stack contents are irrelevant, just need to end the string in a final
state.
Example
\(L = \{a^nb^n | n \ge 0\}, \Sigma = \{a, b\}, \Gamma = \{z,a\}\)
Trace aaabbb
\[\begin{split}\begin{array}{lcccccccc}
&&&&a \\
&&&a&a &a \\
& &a&a&a&a &a \\
\mbox{Stack:} &\underline{z} &\underline{z} &\underline{z} &\underline{z}
&\underline{z} & \underline{z} &\underline{z} &\underline{\ \ \ } \\
\\
\mbox{Unread} \\
\mbox{input:} & aaabbb &aabbb &abbb &bbb & bb & b \\
\end{array}\end{split}\]
Language Acceptance in PDA
Another Definition for Language Acceptance:
NPDA \(M\) accepts \(L(M)\) by empty stack:
\(L(M) = \{w \in \Sigma^* \mid (q_0, w, z) \stackrel{*}{\vdash} (p, \lambda, \lambda)\}\)
Example
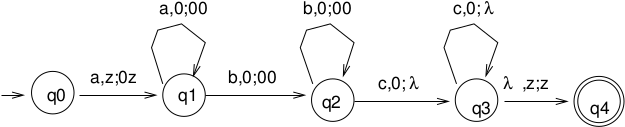
\(L = \{a^nb^mc^{n+m} \mid n,m > 0\}, \Sigma = \{a, b, c\}, \Gamma =\{0, z\}\)
Note: What is the smallest length string that is accepted?
Example
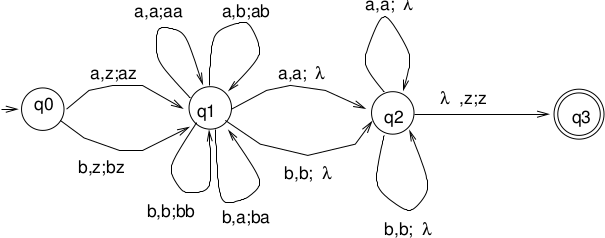
\(L = \{ww^R | w \in \Sigma^+ \}, \Sigma = \{a, b\}, \Gamma = ?\)
Trace abbbba
\[\begin{split}\begin{array}{lcccccccc}
&&&&b \\
&&&b&b &b \\
& &a&a&a&a &a \\
\mbox{Stack:} &\underline{z} &\underline{z} &\underline{z} &\underline{z}
&\underline{z} & \underline{z} &\underline{z} &\underline{\ \ \ } \\
\\
\mbox{Unread} \\
\mbox{input:} & abbbba & bbbba & bbba & bba & ba & a \\
\end{array}\end{split}\]
Example
\(L = \{ww | w \in \Sigma^*\}, \Sigma =\{a, b\}, \Gamma = ?\)
L is not a CFL, so there is no NPDA!
Two Acceptance Definitions
We defined two forms of acceptance:
1. Accept by finishing string in some final state (on some choice
of transitions), no concern with stack state
Oh, and the stack can never actually be empty, there is a
start symbol on stack.
2. Finish string with an empty stack.
We can show that these two are equivalent. (What does equivalent mean?)