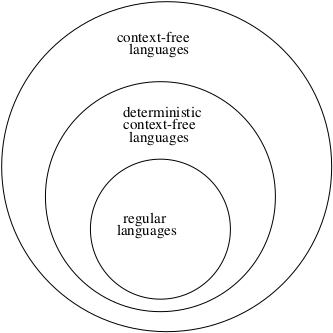
6.Deterministic Pushdown Automata§

Definition: A PDA $M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)$ is deterministic if for every $q \in Q$ , $a \in \Sigma \cup \{\lambda\}$ , $b \in \Gamma$ :

1. $\delta(q, a, b)$ contains at most one element

2. if $\delta(q, \lambda, b)$ is not empty, then $\delta(q, c, b)$ must be empty for every $c \in \Sigma$ .

Definition: $L$ is a deterministic context-free language (DCFL) if and only if there exists a deterministic PDA $M$ such that $L = L(M)$ .

Deterministic Example (1)

The language $L = \{a^nb^n | n \ge 1\}$ is a deterministic CFL.

Proof: The PDA

$M = (\{q_0, q_1, q_2, q_3\}, \{a, b\}, \{0, 1\}, \delta, q_0, Z, \{q_3\})$ with

δ(q0,a,Z)={(q1,1Z)},
δ(q1,a,1)={(q1,11)},
δ(q1,b,1)={(q2,λ)},
δ(q2,b,1)={(q2,λ)},
δ(q2,λ,Z)={(q3,λ)}

accepts the given language.

It satisfies the conditions for being deterministic.

Deterministic Example (2)

Note that this machine DOES have

$\lambda$ transitions.

The key point is that there is still only one choice (because of what is sitting on the top of the stack).

In that sense, it is not merely a “free ride” transition.

Non-deterministic Example

Our previous PDA for $\{ww^R | w\in{\Sigma}^{+}\}, \Sigma = \{a, b\}$ is nondeterministic.

It contains these transitions:

$\delta(q_0, a, a) = \{(q_0, aa)\}$

$\delta(q_0, \lambda, a) = \{(q_1, a)\}$

This violates our conditions for determinism. << Do you see why? >>

Now, this fact that we have a PDA that is not deterministic certainly does not prove that $\{ww^R | w\in{\Sigma}^{+}\}, \Sigma = \{a, b\}$ is not a deterministic CFL.

But, there are CFL’s that are not deterministic. This is one of them.

Another Non-deterministic Example

$L = \{a^nb^n|n \ge 1\} \cup \{a^nb^{2n}| n\ge 1\}$ is a CFL and not a DCFL.

Obviously, both languages are CFL.

And obviously, their union is CFL.

But imagine how the “obvious” NPDA works:

The start state transitions to the “correct” machine to recognize a
string in either language.
But how can we do this deterministically?
We would need a completely different approach to be deterministic.

This is not a proof that the language is not deterministic, but next is one.

Proof (1)

Theorem:

$L = \{a^nb^n: n \ge 1\} \cup \{a^nb^{2n}: n \ge 1\}$ is not a DCFL

(because

$a^nb^nc^n$ is not a CFL).

Proof:

Assume that there is a deterministic PDA

$M$ such that

$L = L(M)$ .

We will construct a PDA that recognizes a language that is not a CFL and derive a contradiction.

Proof (2)

Construct a PDA

$M'$ as follows:

1. Create two copies of M:M1 and M2.
The same state in M1 and M2 are called cousins.
2. Remove accept status from accept states in M1,
remove initial status from initial state in M2.
In new PDA, we will start in M1 and accept in M2.
3. Outgoing arcs from old accept states in M1,
change to end up in the cousin of its destination in
M2.
This joins M1 and M2 into one PDA.
There must be an outgoing arc since you must recognize
both anbn and anb2n.
After reading n b’s, must accept if no more b’s and
continue if there are more b’s.
4. Modify all transitions that read b, have their
destinations in M2 to read c.

This is the construction of our new PDA.

Proof (3)

When we read

$a^nb^n$ and end up in an old accept state in

$M_1$ , then we will transfer to

$M_2$ and read the rest of

$a^nb^{2n}$ . Only the b’s in

$M_2$ have been replaced by c’s, so the new machine accepts

$a^nb^nc^n$ .

The language accepted by our new PDA is

$a^nb^nc^n$ . But this is not a CFL. Contradiction! Thus there is no deterministic PDA

$M$ such that

$L(M) = L$ .

A New Model of the FL Universe

Based on this information, we now can update our model of the Formal Languages Universe.