4.Transforming CFGs (1)§

We use grammars to represent a programming language.
Want to know: Is a given string (or program \(x\)) valid
(syntactically correct)?
Same as asking if it is in the language.

We have seen that (with restrictions on form of CFG), we can determine whether \(w\) is in \(L(G)\) in \(2|w|\) rounds, each step adding a terminal or increasing in length.

This works, but it is not fast enough, that is, not linear!

Transforming CFGs (2)

Key question: Are there ways to transform (restrict) CFGs such that

1) We can process efficiently

2) without restricting the power of CFGs

<< What does it mean “without restricting the power of CFGs”? >>

Specifically, we look at restrictions on the right hand side of the production rules.

Need to be able to automatically transform an arbitrary CFG into an equivalent restricted CFG.

Substitution Theorem (1)

Sometimes it is easier to reason about grammars for languages without \(\lambda\).

(Besides, its pointless to keep expanding on productions that derive to the empty string.)

Useful note: It would be easy to add \(\lambda\) to any grammar by adding a new start symbol \(S_0\),

\(S_0 \rightarrow S \mid \lambda\)

So in practice, if we can transform grammar \(G\) into \(\hat{G}\) such that \(L(\hat{G}) = L(G) - \{\lambda\}\), then the two are effectively equivalent.

Substitution Theorem (2)

Let \(G\) be a CFG. Suppose \(G\) contains \(A \rightarrow x_1Bx_2\)

where \(x_i \in (V \cup T)^{*}\), \(A\) and \(B\) are different variables, and \(B\) has the productions

\(B \rightarrow y_1|y_2|\ldots|y_n\).

We can construct \(G'\) from \(G\) by deleting

\(A \rightarrow x_1Bx_2\)

from \(P\) and adding to it

\(A \rightarrow x_1y_1x_2|x_1y_2x_2|\ldots | x_1y_nx_2\).

Substitution Theorem: \(L(G) = L(G')\).

Substitution Theorem Example

Grammar \(G\):

\(A \rightarrow a \mid aaA \mid abBc\)

\(B \rightarrow abbA \mid b\)

Substitute to get \(\hat{G}\):

\(A \rightarrow a \mid aaA \mid ababbAc \mid abbc\)

\(B \rightarrow abbA \mid b\)

Then the B productions become useless productions.

<< Question: Why don’t we also delete \(B\) rules? >>

Substitution Theorem Example

What was the point to this? Look at derivations.

Derivation under \(G\) for \(aaabbc\):

\(A \Rightarrow aaA \Rightarrow aaabBc \Rightarrow aaabbc\)

Derivation under \(\hat{G}\) for \(aaabbc\):

\(A \Rightarrow aaA \Rightarrow aaabbc\)

Useless Productions (1)

We left in the productions for \(B\), but maybe there is no way remaining to reach them. Obviously they can go.

This example is not as obvious:

\(S \rightarrow aSb \mid \lambda \mid A\)

\(A \rightarrow aA\)

Definition: Variable \(A \in V\) is said to be useful if and only if there is at least one \(w \in L(G)\) such that

\(S \stackrel{*} \Rightarrow xAy \stackrel{*} \Rightarrow w\)

We want to eliminate both types of useless production.

Theorem: (useless productions)

Let \(G\) be a CFG.

Then there exists \(\hat{G}\) that does not contain any useless variables or productions such that \(L(G) = L(\hat{G})\).

Process (1)

To Remove Useless Productions:

Let \(G = (V,T,S,P)\).

I. Compute \(V_1 =\) {Variables that can derive strings of terminals}

1. \(V_1 = \emptyset\)

2. Repeat until no more variables added

* For every \(A \in V\) with \(A \rightarrow x_1x_2\ldots x_n\), all \(x_i \in (T^* \cup V_1)\), add \(A\) to \(V_1\)

3. Take \(P_1\) as all productions in \(P\) whose symbols are all in \((V_1 \cup T)\)

Then \(G_1 = (V_1, T, S, P_1)\) has no variables that can’t derive strings.

NOTE: Now need to get rid of productions we can’t use.

Example (1)

\(S \rightarrow aB \mid bA\)
\(A \rightarrow aA\)
\(B \rightarrow Sa \mid b\)
\(C \rightarrow cBc \mid a\)
\(D \rightarrow bCb\)
\(E \rightarrow Aa \mid b\)

We process this to eliminate \(A\).

Process (2)

II. Draw Variable Dependency Graph

For \(A \rightarrow xBy\), draw \(A \rightarrow B\).
Draw \(A\) in a circle, \(B\) in a circle, and an arc from
\(A\) to \(B\).
Remove productions for \(V\) if there is no path from \(S\) to
\(V\) in the dependency graph.
Resulting Grammar \(G'\) is such that \(L(G) = L(G')\) and
\(G'\) has no useless productions.

Example (2)

\(S \rightarrow aB\)
\(B \rightarrow Sa \mid b\)
\(C \rightarrow cBc \mid a\)
\(D \rightarrow bCb\)
\(E \rightarrow Aa \mid b\)

Example (2)

\(G_1\):

\(S \rightarrow aB\)
\(B \rightarrow Sa \mid b\)
\(C \rightarrow cBc \mid a\)

Now, do it again.

\(G'\):

\(S \rightarrow aB\)

\(B \rightarrow Sa \mid b\)

Removing \(\lambda\) Productions

NOTE: Last time talked about simpler CFG that had no \(\lambda\)-productions, now we will show how to get rid of them.

Theorem (remove \(\lambda\) productions)
Let \(G\) be a CFG with \(\lambda\) not in \(L(G)\).
Then there exists a CFG \(G'\) having no
\(\lambda\)-productions such that \(L(G) = L(G')\).

Process: Removing \(\lambda\) Productions

1. Let \(V_n = \{A \mid \exists\ \mbox{production}\ A \rightarrow \lambda\}\)

2. Repeat until no more additions

* if \(B \rightarrow A_1A_2 \ldots A_m\) and \(A_i \in V_n\) for all \(i\), then put \(B\) in \(V_n\)

THUS, \(V_n = \{A \mid A\stackrel{*}{\Rightarrow} \lambda \}\)

3. Construct \(G'\) with productions \(P'\) such that

* If \(A \rightarrow x_1x_2\ldots x_m \in P, m \ge 1\), then put all productions formed when \(x_j\) is replaced by \(\lambda\) (for all \(x_j \in V_n\)) such that \(|\mbox{rhs}| \ge 1\) into \(P'\).

Example

\(S \rightarrow Ab\)
\(A \rightarrow BCB \mid Aa\)
\(B \rightarrow b \mid \lambda\)
\(C \rightarrow cC \mid \lambda\)

\(G'\):

\(S \rightarrow Ab \mid b\)
\(A \rightarrow BCB \mid BC \mid BB \mid CB \mid B \mid C \mid Aa \mid a\)
\(B \rightarrow b\)
\(C \rightarrow cC \mid c\)

NOTE: Don’t add \(A \rightarrow \lambda\)!

Unit Productions

Definition: Unit Production:

\(A \rightarrow B\)

where \(A, B \in V\).

Consider removing unit productions: Suppose we have

\(A \rightarrow B\)

\(B \rightarrow a \mid ab\)

This becomes: \(A \rightarrow a \mid ab\)

Unit Productions (2)

But what if we have

\(A \rightarrow B \quad\) becomes \(\quad A \rightarrow C\)
\(B \rightarrow C \qquad\qquad\qquad\qquad B \rightarrow A\)
\(C \rightarrow A \qquad\qquad\qquad\qquad C \rightarrow B\)

But we didn’t get rid of unit productions!

Removing Unit Productions

Theorem (Remove unit productions)
Let \(G = (V, T, S, P)\) be a CFG without
\(\lambda\)-productions.
Then there exists CFG \(G' = (V', T', S, P')\) that does not
have any unit-productions and \(L(G) = L(G')\).

Process

1. Find for each \(A\), all \(B\) such that \(A \stackrel{*}{\Rightarrow} B\)

(Draw a dependency graph howing relationship of Unit productions. Just draw arc for each \(A \rightarrow B\) rule.

Draw \(A\) in a circle, \(B\) in a circle, and an arc from \(A\) to \(B\).)

2. Construct \(G' = (V', T', S, P')\) by

(a) Put all non-unit productions in \(P'\)

(b) For all \(A \stackrel{*}{\Rightarrow} B\) such that \(B \rightarrow y_1 \mid y_2 \mid \ldots y_n \in P'\), put \(A \rightarrow y_1 \mid y_2 \mid \ldots y_n \in P'\)

Run DFS with \(A\) as root.

Note the star in \(A \stackrel{*}{\Rightarrow} B\)

Never put a unit production in \(P'\).

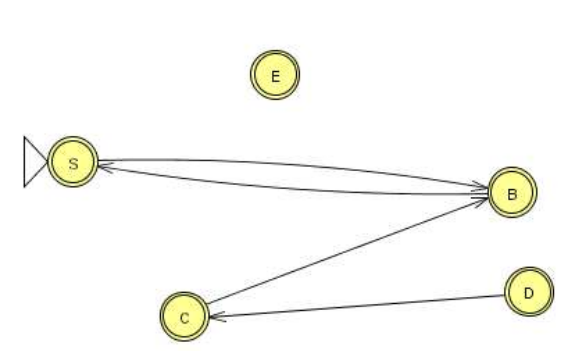
Example (1)

Original:

\(S \rightarrow Aa \mid B\)
\(B \rightarrow A \mid bb\)
\(A \rightarrow a \mid bc \mid B\)

Unit Production Dependency Graph:

Example (2)

Remove the unit production rules, and add these rules:

\(S \rightarrow a \mid bc \mid bb\)
\(A \rightarrow bb\)
\(B \rightarrow a \mid bc\)

Result:

\(S \rightarrow a \mid bc \mid bb \mid Aa\)
\(A \rightarrow a \mid bb \mid bc\)
\(B \rightarrow a \mid bb \mid bc\)

Theorem

Theorem: Let \(L\) be a CFL that does not contain \(\lambda\). Then there exists a CFG for \(L\) that does not have any useless productions, \(\lambda\)-productions, or unit-productions.

Proof:

Remove \(\lambda\)-productions
Remove unit-productions
Remove useless productions

Order is important. Removing \(\lambda\)-productions can create unit-productions!

There are additional examples in the book.

Chomsky Normal Form (CNF)

Definition: A CFG is in Chomsky Normal Form (CNF) if all productions are of the form

\(A \rightarrow BC\) or \(A \rightarrow a\)

where \(A, B, C \in V\) and \(a \in T\).

Why would you want to put a grammar in this form?

Because it is easier to work with (reason about), so will see it in future.

Theorem:

Any CFG \(G\) with \(\lambda\) not in \(L(G)\) has an equivalent grammar in CNF.

Proof:

1. Remove \(\lambda\)-productions, unit productions, and useless productions. (We already know how to do this.)

2. For every right-hand-side of length \(> 1\), replace each terminal \(x_i\) by a new variable \(C_j\) and add the production \(C_j \rightarrow x_i\).

Note: All productions are in the correct form or the right-hand-side is a string of variables.

3. Replace every right-hand-side of length \(> 2\) by a series of productions, each with right-hand-side of length 2.

Example (1)

\(S \rightarrow CBcd\)
\(B \rightarrow b\)
\(C \rightarrow Cc \mid e\)

(after step 1)
\(S \rightarrow CBC_1C_2\)
\(B \rightarrow b\)
\(C \rightarrow CC_3 \mid e\)
\(C_1 \rightarrow c\)
\(C_2 \rightarrow d\)
\(C_3 \rightarrow c\)

Example (2)

(after step 2):
\(S \rightarrow CZ_1\)
\(Z_1 \rightarrow BZ_2\)
\(Z_2 \rightarrow C_1C_2\)
\(B \rightarrow b\)
\(C \rightarrow CC_3 \mid e\)
\(C_1 \rightarrow c\)
\(C_2 \rightarrow d\)
\(C_3 \rightarrow c\)

NOTE: Can get rid of \(\lambda\)-productions and unit productions first!

Greibach Normal Form (GNF)

Definition: A CFG is in Greibach normal form (GNF) if all productions have the form

\(A \rightarrow ax\)

where \(a \in T\) and \(x \in V^*\)

This is like an s-grammar (or simple grammar, Linz page 144), except the s-grammar definition includes a further restriction that any pair \((A, a)\) can occur at most in one rule.

This is so that you wouldn’t have to backtrack (only one choice to match the derivation of a string). So it is very restrictive.

GNF Theorem

For every CFG \(G\), there exists a grammar in GNF.

See proof in book.

Example:

\(S \rightarrow AB\)
\(A \rightarrow aA \mid bB \mid b\)
\(B \rightarrow b\)

Simple substitutions give us:

\(S \rightarrow aAB \mid bBB \mid bB\)
\(A \rightarrow aA \mid bB \mid b\)
\(B \rightarrow b\)

What You Should Know

Know what usless productions, unit productions, etc. are
Don’t memorize the processes for eliminating them, but
understand how they work in principle.
Know what the GNF and CNF forms are.