6.Which of these is a CFL?§

Which of the following languages are CFL?

L={anbncj∣0<n≤j}

L={anbjanbj∣n>0,j>0}

L={anbjakbp∣n+j≤k+p,n>0,j>0,k>0,p>0}

L={anbjajbn∣n>0,j>0}

Pumping Lemma: Regular Languages

Let

$L$ be an infinite regular language.

Then there exists a constant

$m > 0$ such that any

$w \in L$ with

$|w| \ge m$ can be decomposed into three parts as

$w=xyz$ with:

|xy|≤m
|y|≥1
xyiz∈L for all i≥0

With this pumping lemma, we were able to show that $a^nb^n$ is not a regular language.

Pumping Lemma for CFLs: Intuition

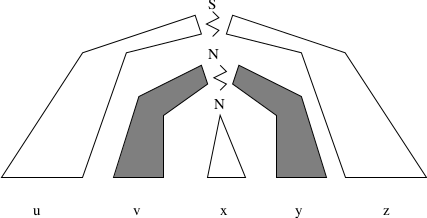
Suppose a variable repeats, such as: $A \stackrel{*}{\Rightarrow} vAy$ , with $A \stackrel{*}{\Rightarrow} x$ .

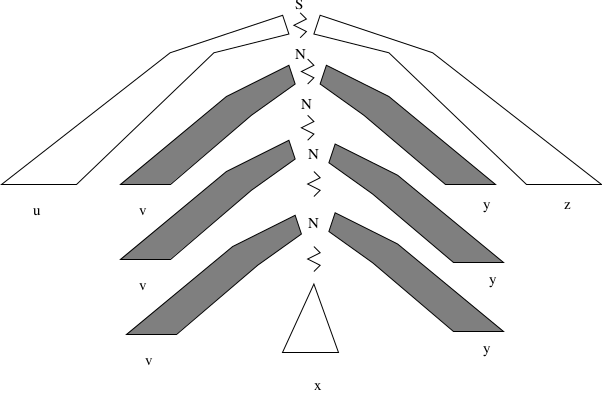
The derived string will then contain the substring $vxy$ . There will also be strings in the language that contain substrings $x, vvxyy, vvvxyyy...$

A little more complicated because there can be two “pumped” parts (in equal measure of pumped-ness).

Pumping Lemma for CFLs

Let

$L$ be any infinite CFL.

Then exists a constant

$m$ (depending only on

$L$ ), such that for every string

$w \in L$ , with

$|w| \ge m$ , we may partition

$w = uvxyz$ such that:

$|vxy| \le m$ , (limit on size of substring)

$|vy| \ge 1$ , (

$v$ and

$y$ not both empty)

for all

$i \ge 0, uv^ixy^iz \in L$

Proof Sketch (1)

There is a CFG $G$ such that $L = L(G)$ .

Consider the parse tree of a long string in $L$ .

For any long string, some nonterminal $N$ must appear twice in the path.

Proof Sketch (2)

N∗⇒vNy and
N∗⇒x.
S∗⇒uNz∗⇒uvNyz∗⇒uvxyz
By repeating the v and y subtrees, get
N∗⇒viNyi∗⇒vixyi.

<< How does this work for grammar $S \rightarrow aSb | ab$ ? >>

Proof Example Problem

Consider $L = \{a^nb^nc^n: n\ge 1\}$ .

Why would we want to recognize the language $\{a^nb^nc^n: n\ge 1\}$ ?

Recognize underlined words:

$\underline{word}$ is stored as $word\beta\beta\beta\beta\ \_\ \_\ \_\ \_$ where $\beta$ represents a backspace.

Unfortunately, $L$ is not a CFL.

Proof (1)

Assume L is a CFL and apply the pumping lemma.
Let m be the constant in the pumping lemma and consider
w=ambmcm.
Note |w|≥m.
Show there is no division of w into uvxyz such
that |vy|≥1, |vxy|≤m, and
uvixyiz∈L for i=0,1,2,….

Case 1: Neither v nor y can contain 2 or more
distinct symbols.
If v contains a’s and b’s,
then uv2xy2z∉L since there will be b’s
before a’s.
Thus, v and y can be only a’s,
b’s, or c’s (not mixed).

Proof (2)

Case 2: v=at1, then y=at2
or bt3, (|vxy|≤m)
If y=at2,
then uv2xy2z=am+t1+t2bmcm∉L since
t1+t2>0,n(a)>n(b) (number of a’s is
greater than number of b’s)
If y=bt3, then
uv2xy2z=am+t1bm+t3cm∉L
since t1+t3>0, either n(a)>n(c) or
n(b)>n(c).

Case 3: v=bt1, then y=bt2 or ct3.
If y=bt2, then uv2xy2z=ambm+t1+t2cm∉L
since t1+t2>0,n(b)>n(a).
If y=ct3, then
uv2xy2z=ambm+t1cm+t3∉L
since t1+t3>0, either n(b)>n(a) or
n(c)>n(a).

Proof (3)

Case 4: v=ct1, then y=ct2.
Then, uv2xy2z=ambmcm+t1+t2∉L
since t1+t2>0,n(c)>n(a).

Thus, there is no breakdown of w into uvxyz such
that |vy|≥1, |vxy|≤m and for all
i≥0, uvixyiz is in L.
This is a contradiction, thus, L is not a CFL.

Adversary Version (1)

Adversary picks some value for

$m$ .

We pick the string

$w = a^mb^mc^m$ .

Adversary picks the breakdown for

$w = uvxyz$ . Adversary has (bad) choices:

$vxy$ are all a’s, or all b’s, or all c’s.

This cannot be pumped.

$vxy$ has either

$v$ or

$y$ a mix of letters

This cannot be pumped.

$vy$ has between them an equal number of a’s, b’s, and c’s.

This is too long.

Adversary Version (2)

Note that both

$v$ and

$y$ are pumped the same number of times.

If the adversary could pick them with this in mind, then the string might be pumpable.

For example, if

$v = a^k$ and

$y = b^kc^k$ .

But the length restriction kicks in to prevent that.

(Try to) Prove a CFL not a CFL

What if we try to prove that $L = a^nb^n$ is not context free, by using the pumping lemma?

Pick $w = a^mb^m$ .

Adversary picks $v = a^k$ and $y = b^k$ .

Of course, this does not prove that $L$ is context free. Just that we failed to disprove this with the pumping lemma (that is a good thing).

Example

Prove that $L = \left\{ ww \mid w \in \{a, b\}^* \right\}$ is not a CFL.

Consider the string $w = a^mb^ma^mb^m$ .

No matter how the adversary picks

$vxy$ , it is not pumpable.

Example

Prove that $L \left\{ a^{n!} \mid n \geq 0 \right\}$ is not a CFL.

We pick w=am!.
Obviously, any decomposition is of the form v=ak,
y=al.
This is not pumpable.