12.1. B-Trees¶
12.1.1. B-Trees¶
12.1.1.1. B-Trees (1)¶
The B-Tree is an extension of the 2-3 Tree.
The B-Tree is now the standard file organization for applications requiring insertion, deletion, and key range searches.
Databases
File Systems
12.1.1.2. B-Trees (2)¶
B-Trees are always balanced.
B-Trees keep similar-valued records together on a disk page, which takes advantage of locality of reference.
B-Trees guarantee that every node in the tree will be full at least to a certain minimum percentage. This improves space efficiency while reducing the typical number of disk fetches necessary during a search or update operation.
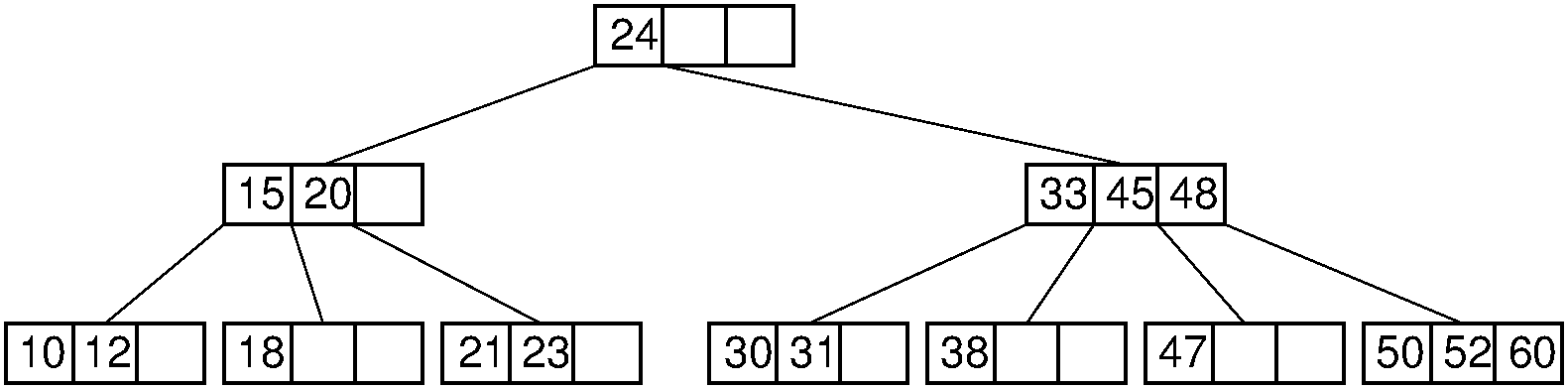
12.1.1.3. B-Tree Definition¶
- A B-Tree of order \(m\) has these properties:
The root is either a leaf or has two children.
Each node, except for the root and the leaves, has between \(\lceil m/2 \rceil\) and \(m\) children.
All leaves are at the same level in the tree, so the tree is always height balanced.
A B-Tree node is usually selected to match the size of a disk block.
A B-Tree node could have hundreds of children.
12.1.1.4. B-Tree Search¶
- Generalizes search in a 2-3 Tree.
Do binary search on keys in current node. If search key is found, then return record. If current node is a leaf node and key is not found, then report an unsuccessful search.
Otherwise, follow the proper branch and repeat the process.
12.1.1.5. B+-Trees¶
The most commonly implemented form of the B-Tree is the B+-Tree.
Internal nodes of the B+-Tree do not store record – only key values to guild the search.
Leaf nodes store records or pointers to records.
A leaf node may store more or less records than an internal node stores keys.
12.1.1.6. 23+-Tree Build Example¶
12.1.1.7. 23+-Tree Search Example¶
12.1.1.8. 23+-Tree Delete Example¶
12.1.1.9. B+-Tree Find¶
12.1.1.10. B+-Tree Insert¶
12.1.1.11. B+-Tree Deletion¶
12.1.1.12. B+-Tree Insert (Degree 5)¶
12.1.1.13. B-Tree Space Analysis (1)¶
B+-Trees nodes are always at least half full.
The B*-Tree splits two pages for three, and combines three pages into two. In this way, nodes are always 2/3 full.
Asymptotic cost of search, insertion, and deletion of nodes from B-Trees is \(\Theta(log n)\).
Base of the log is the (average) branching factor of the tree.
12.1.1.14. B-Tree Space Analysis (2)¶
Example: Consider a B+-Tree of order 100 with leaf nodes containing 100 records.
1 level B+-tree:
2 level B+-tree:
3 level B+-tree:
4 level B+-tree:
- Ways to reduce the number of disk fetches:
Keep the upper levels in memory.
Manage B+-Tree pages with a buffer pool.
12.1.1.15. B-Trees: The Big Idea¶
B-trees are really good at managing a sorted list
They break the list into manageable chunks
The leaves of the B+-tree form the list
The internal nodes of the B+-tree merely help find the right chunk